Giải và biện luận các hệ bất phương trình
a)
\(\left\{ \matrix{
(x - \sqrt 5 )(\sqrt 7 - 2x) > 0 \hfill \cr
x - m \le 0 \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
{2 \over {x - 1}} < {5 \over {2x - 1}} \hfill \cr
x - m \ge 0 \hfill \cr} \right.\)
Đáp án
a) Ta có bảng xét dấu:
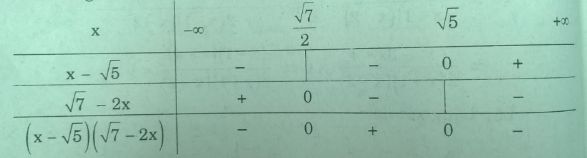
Vậy \((x - \sqrt 5 )(\sqrt 7 - 2x) > 0 \Leftrightarrow {{\sqrt 7 } \over 2} < x < \sqrt 5 \)
Ta có: \({S_1} = ({{\sqrt 7 } \over 2};\sqrt 5 )\)
Bất phương trình thứ hai có nghiệm \(x ≤ m\).
Ta có: \({S_2} = (-∞; m]\),
Do đó:
+ Nếu \(m \le {{\sqrt 7 } \over 2}\) thì tập nghiệm là S = S1 ∩ S2 = Ø
Advertisements (Quảng cáo)
+ Nếu \({{\sqrt 7 } \over 2} \le m < \sqrt 5 \) thì tập nghiệm là \(S = {S_1} \cap {S_2} = ({{\sqrt 7 } \over 2},m)\)
+ Nếu \(m \ge \sqrt 5 \) thì tập nghiệm là \(S = {S_1} \cap {S_2} = ({{\sqrt 7 } \over 2}\sqrt 5 )\)
b) Ta có:
\({2 \over {x - 1}} < {5 \over {2x - 1}} \Leftrightarrow {{2(2x - 1) - 5(x - 1)} \over {(x - 1)(2x - 1)}} < 0 \Leftrightarrow {{x - 3} \over {(x - 1)(2x - 1)}} > 0\)
Bằng cách lập bảng xét dấu vế trái, ta có:
\({2 \over {x - 1}} < {5 \over {2x - 1}} \Leftrightarrow \left[ \matrix{
{1 \over 2} < x < 1 \hfill \cr
x > 3 \hfill \cr} \right.\)
Ta có: \({S_1} = ({1 \over 2};1) \cup (3, + \infty )\)
Tập nghiệm của bất phương trình thứ hai là: S2 = [m, +∞ )
Do đó:
+ Nếu \(m \le {1 \over 2}\) thì tập nghiệm là \({S_1} = ({1 \over 2};1) \cup (3, + \infty )\)
+ Nếu \({1 \over 2} < m < 1\) thì tập nghiệm là \(S = {\rm{[m, 1)}} \cup {\rm{(3, + }}\infty {\rm{)}}\)
+ Nếu \(1≤ m ≤ 3\) thì tập nghiệm là \(S = (3, +∞ )\)
+ Nếu \(m > 3\) thì tập nghiệm là \(S = [m; +∞ )\)
