Giải các bất phương trình sau:
a) \({{{x^2} - 9x + 14} \over {{x^2} - 5x + 4}} > 0\)
b) \({{ - 2{x^2} + 7x + 7} \over {{x^2} - 3x - 10}} \le - 1\)
c) (2x + 1)(x2 + x – 30) ≥ 0
d) x4 – 3x2 ≤ 0
Đáp án
a) Ta có:
\(\eqalign{
& {x^2} - 9x + 14 = 0 \Leftrightarrow \left[ \matrix{
x = 2 \hfill \cr
x = 7 \hfill \cr} \right. \cr
& {x^2} - 5x + 4 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = 4 \hfill \cr} \right. \cr} \)
Bảng xét dấu:
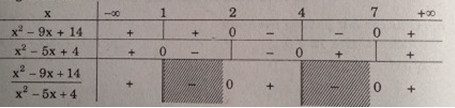
Vậy \(S = (-∞, 1) ∪ (2, 4) ∪ (7, +∞)\)
b) Ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& {{ - 2{x^2} + 7x + 7} \over {{x^2} - 3x - 10}} \le - 1\cr& \Leftrightarrow {{ - 2{x^2} + 7x + 7} \over {{x^2} - 3x - 10}} + 1 \le 0 \Leftrightarrow {{ - {x^2} + 4x - 3} \over {{x^2} - 3x - 10}} \le 0 \cr} \)
Ta lại có:
\(\eqalign{
& - {x^2} + 4x - 3 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = 3 \hfill \cr} \right. \cr
& {x^2} - 3x - 10 = 0 \Leftrightarrow \left[ \matrix{
x = 5 \hfill \cr
x = - 2 \hfill \cr} \right. \cr} \)
Bảng xét dấu:
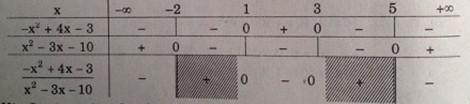
Vậy \(S = (-∞, -2) ∪ [1, 3] ∪ (5, +∞)\)
c) Bảng xét dấu:
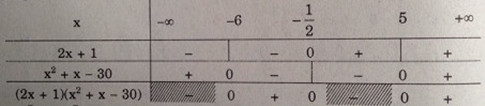
Vậy \(S = {\rm{[}} - 6,\, - {1 \over 2}{\rm{]}} \cup {\rm{[}}5,\, + \infty )\)
d) Ta có:
\(\eqalign{
& {x^4} - 3{x^2} \le 0 \Leftrightarrow {x^2}({x^2} - 3) \le 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
{x^2} - 3 \le 0 \hfill \cr} \right. \cr
& \Leftrightarrow - \sqrt 3 \le x \le \sqrt 3 \cr} \)
Vậy \(S = {\rm{[}} - \sqrt 3 ,\,\sqrt 3 {\rm{]}}\)
