Advertisements (Quảng cáo)
Tìm các giá trị của m để hệ bất phương trình sau có nghiệm:
\(\left\{ \matrix{
{x^2} + 2x – 15 < 0 \hfill \cr
(m + 1)x \ge 3 \hfill \cr} \right.\)
Đáp án
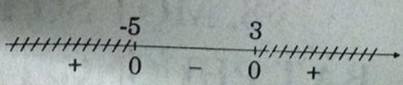
Ta có: x2 + 2x – 15 < 0 ⇔ -5 < x < 3
Ta xét bất phương trình: (m + 1)x ≥ 3 (*)
+ Nếu m = -1 thì S = Ø
+ Nếu m > -1 thì: \((*) \Leftrightarrow x \ge {3 \over {m + 1}}\)
Hệ có nghiệm:
Advertisements (Quảng cáo)
\( \Leftrightarrow \left\{ \matrix{
{3 \over {m + 1}} < 3 \hfill \cr
m > – 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
m > 0 \hfill \cr
m > – 1 \hfill \cr} \right. \Leftrightarrow m > 0\)
+ Nếu m < -1 thì \((*) \Leftrightarrow x \le {3 \over {m + 1}}\)
Hệ có nghiệm:
\( \Leftrightarrow \left\{ \matrix{
{3 \over {m + 1}} > – 5 \hfill \cr
m + 1 < 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
3 < – 5m – 5 \hfill \cr
m < – 1 \hfill \cr} \right. \Leftrightarrow m < – {8 \over 5}\)
Vậy hệ có nghiệm khi và chỉ khi:
\(\left[ \matrix{
m < – {8 \over 5} \hfill \cr
m > 0 \hfill \cr} \right.\)