Bài 7. Cho bốn điểm bất kì \(A, B, C, D\). Chứng minh rằng
\(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0\).
Từ đó suy ra một cách chứng minh định lí: “Ba đường cao của một tam giác đồng quy”.

Advertisements (Quảng cáo)
Ta có
\(\eqalign{
& \,\,\,\,\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \cr
& = \overrightarrow {DA} (\overrightarrow {DC} - \overrightarrow {DB} ) + \overrightarrow {DB} (\overrightarrow {DA} - \overrightarrow {DC} ) + \overrightarrow {DC} (\overrightarrow {DB} - \overrightarrow {DA} ) \cr
& = \overrightarrow {DA} \overrightarrow {DC} - \overrightarrow {DA} \overrightarrow {DB} + \overrightarrow {DB} \overrightarrow {DA} - \overrightarrow {DB} \overrightarrow {DC} + \overrightarrow {DC} \overrightarrow {DB} - \overrightarrow {DC} \overrightarrow {DA} = 0 \cr} \)
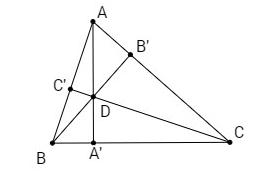
Gọi \(D\) là giao điểm của hai đường cao \(AA’, BB’\) của tam giác \(ABC\).
Ta có \(\overrightarrow {DA} .\overrightarrow {BC} = 0\,;\,\,\overrightarrow {DB} .\overrightarrow {CA} = 0\)
Từ đó suy ra \(\overrightarrow {DC} .\overrightarrow {AB} = 0\), do đó \(DC \bot AB\). Vậy \(D\) nằm trên đường cao \(CC’\) của tam giác \(ABC\), tức là ba đường cao trong tam giác đồng quy.
