Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ.
Khẳng định nào sau đây là đúng?
a) \(|\overrightarrow {OA} + \overrightarrow {OB} | = AB\)
b)
\(\left\{ \matrix{
\overrightarrow {OA} - \overrightarrow {OB} \hfill \cr
\overrightarrow {DC} \hfill \cr} \right.\)
cùng hướng
c) xA = -xC và yA = yC
d) xB = -xC và yC = -yB
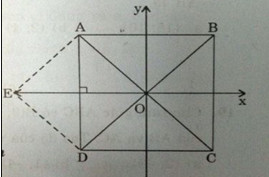
a) Qua A kẻ \(\overrightarrow {AE} = \overrightarrow {OB} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {AE} = \overrightarrow {OE} \)
Advertisements (Quảng cáo)
Ta dễ dàng chứng minh được:
\(\overrightarrow {OE} = \overrightarrow {BA} \Rightarrow |\overrightarrow {OA} + \overrightarrow {OB} | = |\overrightarrow {OE} | = |\overrightarrow {BA} | = AB\)
Vậy a) đúng
b) Vì \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \)
Mà \(\overrightarrow {BA} \) và \(\overrightarrow {DC} \) ngược hướng nên b) sai
c) xA = -xC và yA = yC là sai.
Đúng ra là : xA = -xC và yA = - yC
d) Sai vì xB = xC
Vậy chọn A.
