Câu 27 trang 32 SGK Hình học 10: Ôn tập Chương I - Vectơ. Các điểm M(2, 3); N(0, -4); P(-1, 6) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC. Tọa độ của đỉnh A là:
Bài 27. Các điểm \(M(2; 3); N(0; -4); P(-1; 6)\) lần lượt là trung điểm các cạnh \(BC, CA, AB\) của tam giác \(ABC\). Tọa độ của đỉnh \(A\) là:
a) \((1; 5)\) b) \((-3; 1)\)
c) \((-2; -7)\) d) \((1; -10)\)
Advertisements (Quảng cáo)
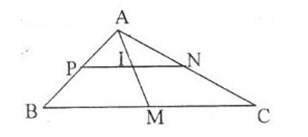
Trung tuyến \(AM\) cắt \(PN\) tại \(I\) thì \(I\) là trung điểm của \(PN\) nên \(I( - {1 \over 2},1)\) và \(I\) cũng là trung điểm của \(AM\).
Suy ra: \(A\) đối xứng với \(M\) qua \(I\) nên:
\(\left\{ \matrix{
{x_A} + {x_M} = 2{x_I} \hfill \cr
{y_A} + {y_M} = 2{y_I} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_A} = 2{x_I} - {x_M} = - 3 \hfill \cr
{y_A} = 2{y_I} - {y_M} = - 1 \hfill \cr} \right.\)
Vậy \(A(-3, -1) ⇒\) chọn B.