Bài 8, Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây là đúng?
A. \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {BC} \)
B. \(\overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} \)
C. \(\overrightarrow {AC} - \overrightarrow {BD} = 2\overrightarrow {CD} \)
D. \(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {CD} \)
Advertisements (Quảng cáo)
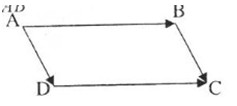
Ta có: tứ giác \(ABCD\) là hình bình hành nên:
\(\left\{ \matrix{
\overrightarrow {AB} = \overrightarrow {DC} \hfill \cr
\overrightarrow {AD} = \overrightarrow {BC} \hfill \cr} \right.\)
\(\eqalign{
& \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} +\overrightarrow {AD}+ \overrightarrow {BC} + \overrightarrow {CD} = 2\overrightarrow {BC} \cr
& \overrightarrow {AC} + \overrightarrow {BC} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {BC} = \overrightarrow {AB} + 2\overrightarrow {BC} \ne \overrightarrow {AB} \cr
& \overrightarrow {AC} - \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {BC} - \overrightarrow {BC} - \overrightarrow {CD} = \overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {AB} \ne 2\overrightarrow {CD} \cr
& \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} - \overrightarrow {BC} = \overrightarrow {AB} \ne \overrightarrow {CD} \cr} \)
Vậy A đúng.
