Advertisements (Quảng cáo)
Bài 9. Trong mặt phẳng tọa độ \(Oxy\) cho hình bình hành \(OABC\), \(C\) nằm trên \(Ox\).
Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} \)có tụng độ khác \(0\)
B. \(A\) và \(B\) có tung độ khác nhau
C. \(C\) có hoành độ bằng \(0\)
D. \({x_A} + {x_C} – {x_B} = 0\)
Advertisements (Quảng cáo)
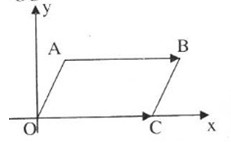
Trong mặt phẳng tọa độ \(O xy\), hình bình hành \(OABC\) có \(C\) nằm trên \(Ox\) nên điểm \(C({x_c};0)\) và \(\overrightarrow {AB} = \overrightarrow {OC} \)
\(⇒ AB//Ox ⇒ A({x_A};m)\) và \(B({x_B};m)\) có cùng tung độ \(m\)
\(\overrightarrow {AB} = ({x_B} – {x_A};0)\) có tung độ bằng \(0\)
Từ \(\overrightarrow {AB} = \overrightarrow {OC} \) suy ra \({x_A} + {x_C} – {x_B} = 0\)
Do đó chọn D.