Cho hàm số\(f(x) = \tan (\pi x)\).
a) Tìm tập xác định của hàm số \(y = f(x)\);
b) Chứng minh rằng với mọi số nguyên k , ta có \(f(x + k) = f(x)\) . Từ đó suy ra \(y = f(x)\) là hàm số tuần hoàn với chu kì T = 1;
c) Cho biết sự biến thiên của hàm số \(y = f(x)\) trên mỗi khoảng\(\left( { - {1 \over 2} + k;{1 \over 2} + k} \right),k \in Z\);
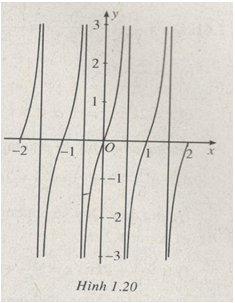
d) Vẽ đồ thị của hàm số đó.
Giải
a) Hàm số \(y = \tan (\pi x)\) xác định khi và chỉ khi \(\cos \left( {\pi x} \right) \ne 0.\) Mặt khác
\(\cos \left( {\pi x} \right) = 0 \Leftrightarrow {\pi x}={\pi \over 2} + k\pi \Leftrightarrow x = {1 \over 2} + k\left( {k \in Z} \right)\)
Từ đó suy ra tập xác định của hàm số \(y = \tan (\pi x)\) là: \(D = R\backslash \left\{ {{1 \over 2} + k|k \in Z} \right\}\)
b) Với mọi \(k \in Z,\) ta có
Advertisements (Quảng cáo)
\(f\left( {x + k} \right) = \tan \left[ {\pi \left( {x + k} \right)} \right] = \tan \left( {\pi x + k\pi } \right) \)
\(= \tan \left( {\pi x} \right) = f\left( x \right)\)
Trong các số nguyên dương, số 1 là nhỏ nhất. Do đó \(\tan (\pi x)\) là hàm số tuần hoàn với chu kì \(T = 1\)
c) Ta thấy
\( - {1 \over 2} + k < x < {1 \over 2} + k \Leftrightarrow - {\pi \over 2} + k\pi < \pi x < {\pi \over 2} + k\pi \)
Từ đó suy ra hàm số \(\tan (\pi x)\) đồng biến trên mỗi khoảng \(\left( { - {1 \over 2} + k;{1 \over 2} + k} \right),\,k \in Z\)
d) Đồ thị của hàm số có dạng như hình 1.20.