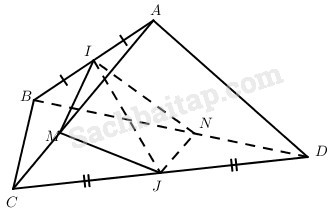
Cho hình tứ diện ABCD; I và J lần lượt là trung điểm của AB và CD; M là điểm thuộc AC sao cho \(\overrightarrow {MA} = {k_1}\overrightarrow {MC} \) ; N là điểm thuộc BD sao cho \(\overrightarrow {NB} = {k_2}\overrightarrow {N{\rm{D}}} \) . Chứng minh rằng các điểm I, J, M, N cùng thuộc một mặt phẳng khi và chỉ khi k1 = k2.

Vì \(\overrightarrow {MA} = {k_1}\overrightarrow {MC} \)
nên \(\overrightarrow {IM} = {{\overrightarrow {IA} - {k_1}\overrightarrow {IC} } \over {1 - {k_1}}}\)
Tương tự, ta có:
\(\overrightarrow {IN} = {{\overrightarrow {IB} - {k_2}\overrightarrow {I{\rm{D}}} } \over {1 - {k_2}}} = {{ - \overrightarrow {IA} - {k_2}\overrightarrow {I{\rm{D}}} } \over {1 - {k_2}}}\)
Mặt khác: \(\overrightarrow {IJ} = {1 \over 2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right)\)
Advertisements (Quảng cáo)
Để các điểm I, I, M, N thuộc một mặt phẳng, điều kiện cần và đủ là ba vectơ \(\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {IJ} \) đồng phẳng. Rõ ràng là \(\overrightarrow {IN} \) và \(\overrightarrow {IJ} \) không cùng phương nên điều khẳng định \(\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {IJ} \) đồng phẳng tương đương với
\(\overrightarrow {IM} = p\overrightarrow {IN} + q\overrightarrow {IJ} \)
hay
\(\eqalign{ & {{\overrightarrow {IA} - {k_1}\overrightarrow {IC} } \over {1 - {k_1}}} = p.{{ - \overrightarrow {IA} - {k_2}\overrightarrow {ID} } \over {1 - {k_2}}} + {q \over 2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right) \cr & \Leftrightarrow \left( {{1 \over {1 - {k_1}}} + {p \over {1 - {k_2}}}} \right)\overrightarrow {IA} - \left( {{{{k_1}} \over {1 - {k_1}}} + {q \over 2}} \right)\overrightarrow {IC} \cr& + \left( {{{p{k_2}} \over {1 - {k_2}}} - {q \over 2}} \right)\overrightarrow {ID} = \overrightarrow 0 \cr} \)
Do \(\overrightarrow {IA} ,\overrightarrow {IC} ,\overrightarrow {ID} \) không đồng phẳng nên đẳng thức trên tương đương với
\(\eqalign{ & \left\{ \matrix{ {1 \over {1 - {k_1}}} + {p \over {1 - {k_2}}} = 0 \hfill \cr {{{k_1}} \over {1 - {k_1}}} + {q \over 2} = 0 \hfill \cr {{p{k_2}} \over {1 - {k_2}}} - {q \over 2} = 0 \hfill \cr} \right. \cr & \Rightarrow {{{k_1}} \over {1 - {k_1}}} = - {{p{k_2}} \over {1 - {k_2}}} = {{{k_2}} \over {1 - {k_1}}} \cr} \)
hay k1 = k2
