14. Trang 7 Sách bài tập Hình Học 11 nâng cao.
Cho đường thẳng a và một điểm I nằm trên nó. Gọi F là phép dời hình biến a thành a và I là điểm duy nhất biến thành chính nó. Chứng minh rằng F biến điểm M bất kì thành điểm M’ sao cho I là trung điểm MM’.

Lấy điểm M bất kì nằm trên a và khác I, phép dời hình F biến a thành a nên biến điểm M thành điểm M’ trên a, IM = IM’. Ngoài ra vì M khác M’ nên I là trung điểm của MM’.
Advertisements (Quảng cáo)
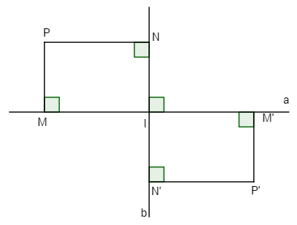
Gọi b là đường thẳng đi qua I, vuông góc với a thì F biến b thành đường thẳng đi qua I và vuông góc với a. Do đó b biến thành b. Cũng lập luận như trên,nếu N nằm trên b thì F biến N thành N’ sao cho I là trung điểm của NN’.
Bây giờ giả sử điểm P không nằm trên a và b. Kẻ \(PM \bot a\) và \(PN \bot b\,\left( {M \in a,\,N \in b} \right)\). Theo chứng minh trên M biến thành M’, N biến thành N’ sao cho I là trung điểm của MM’ và NN’. Suy ra P biến điểm P sao cho M’IN’P là hình chữ nhật và do đó I là trung điểm của PP’.