19. Trang 53 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện đều ABCD có cạnh bằng a. Gọi I là trung điểm của AD, J là điểm đối xứng với D qua C, K là điểm đối xứng với D qua B.
a) Xác định thiết diện của hình tứ diện khi cắt bởi mp(IJK).
b) Tính diện tích thiết diện được xác định bởi câu a.

a) Nối I và J cắt AC tại N. Nối I và K cắt AB tại M. Tam giác IMN là thiết diện cần tìm.
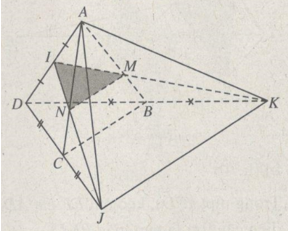
b) Dễ thấy M là trọng tâm tam giác ADK, N là trọng tâm tam giác ADJ. Từ đó ta có:
\(AN = {2 \over 3}AC;\;AM = {2 \over 3}AB\)
Advertisements (Quảng cáo)
Suy ra: \(AN = AM = {2 \over 3}a\) và MN//CB. Do đó \(MN = {2 \over 3}CB\)
hay \(MN = {2 \over 3}a.\)
Xét tam giác AIM. Ta có:
\(\eqalign{
& I{M^2} = A{I^2} + A{M^2} - 2AI.AM.\cos {60^o} \cr
& \,\,\,\,\,\,\,\,\,\,\, = {{{a^2}} \over 4} + {4 \over 9}{a^2} - 2.{a \over 2}.{{2a} \over 3}.{1 \over 2} = {{13} \over {36}}{a^2} \cr
& \Rightarrow IM = {{a\sqrt {13} } \over 6} \cr} \)
Tương tự, ta có \(IN = {{a\sqrt {13} } \over 6}\)
Vậy theo công thức Hê-rông, ta có:
\({S_{IMN}} = \sqrt {\left( {{{a\sqrt {13} } \over 6} + {2 \over 6}a} \right).{2 \over 6}a.{2 \over 6}a.\left( {{{a\sqrt {13} } \over 6} - {2 \over 6}a} \right)} \)
\(= {{{a^2}} \over 6}.\)
