Cho tứ diện ABCD có BC = AD = a, AC = BD = b, AB = CD = c. Đặt α là góc giữa BC và AD; β là góc giữa AC và BD; γ là góc giữa AB và CD. Chứng minh rằng trong ba số hạng \({a^2}\cos \alpha ,{b^2}\cos \beta ,{c^2}\cos \gamma \) có một số hạng bằng tổng hai số hạng còn lại.

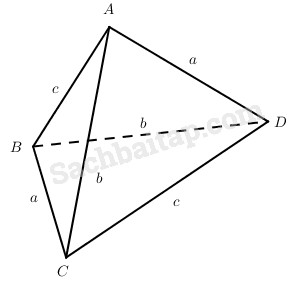
Ta có:
\(\cos \left( {\overrightarrow {BC} ,\overrightarrow {DA} } \right) = {{2{c^2} - 2{b^2}} \over {2{a^2}}} = {{{c^2} - {b^2}} \over {{a^2}}}\).
Vậy nếu góc giữa BC và AD bằng α thì:
\(\cos \alpha = {{\left| {{c^2} - {b^2}} \right|} \over {{a^2}}}\) hay \({a^2}\cos \alpha = \left| {{c^2} - {b^2}} \right|\).
Tương tự như trên, nếu gọi β là góc giữa AC và BD thì:
Advertisements (Quảng cáo)
\({b^2}\cos \beta = \left| {{a^2} - {c^2}} \right|\)
và γ là góc giữa AB và CD thì
\({c^2}\cos \gamma = \left| {{b^2} - {a^2}} \right|\).
Với a, b, c lần lượt là dộ dài của BC, CA, AB, không giảm tính tổng quát có thể coi a ≥ b ≥ c. Khi đó:
\(\eqalign{ & {a^2}\cos \alpha = {b^2} - {c^2} \cr & {b^2}\cos \beta = {a^2} - {c^2} \cr & {c^2}\cos \gamma = {a^2} - {b^2} \cr} \).
Từ đó, trong trường hợp này ta có \({b^2}\cos \beta = {a^2}\cos \alpha + {c^2}\cos \gamma \).
