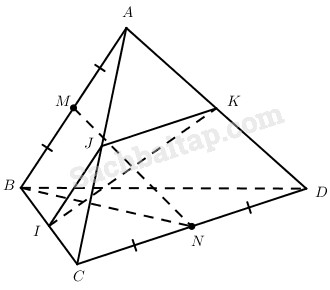
Cho tứ diện ABCD có tất cả các cạnh bằng nhau. Gọi M và N lần lượt là trung điểm của AB và CD. Lấy các điểm I, J, K lần lượt thuộc các đường thẳng BC, AC, AD sao cho \(\overrightarrow {IB} = k\overrightarrow {IC} ,\overrightarrow {J{\rm{A}}} = k\overrightarrow {JC} ,\overrightarrow {K{\rm{A}}} = k\overrightarrow {K{\rm{D}}} \) trong đó k là số khác 0 cho trước. Chứng minh rằng:
a) MN ⊥ IJ và MN ⊥IK
b) AB ⊥ CD

a) Từ
\(\eqalign{ & \overrightarrow {IB} = k\overrightarrow {IC} \cr & \overrightarrow {J{\rm{A}}} = k\overrightarrow {JC} \cr} \)
ta có IJ // AB.
Tương tự, ta có IK // CD.
Advertisements (Quảng cáo)
Do các cạnh của tứ diện ABCD bằng nhau và N là trung điểm của CD nên NA = NB.
Mặt khác MA = MB do đó MN ⊥ AB, suy ra MN ⊥ IJ.
Tương tự như trên, ta có MN ⊥ CD và IK // CD nên MN ⊥ JK.
b) Ta có \(\overrightarrow {AB} = \overrightarrow {AN} + \overrightarrow {NB} \).
Từ giả thiết, ta có:
\(AN \bot C{\rm{D}}\) tức là \(\overrightarrow {AN} .\overrightarrow {C{\rm{D}}} = 0\);
\(BN \bot C{\rm{D}}\) tức là \(\overrightarrow {BN} .\overrightarrow {C{\rm{D}}} = 0\).
Vậy \(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = \left( {\overrightarrow {AN} + \overrightarrow {NB} } \right).\overrightarrow {C{\rm{D}}} = 0\) tức là \(AB \bot C{\rm{D}}\) .
