Câu 26 trang 119 Sách bài tập Hình học 11 Nâng cao. Vậy SO ⊥ mp(ABCD). Bài 2 3 4: Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
Cho hình chóp S.ABCD có đáy là hình bình hành và SA = SC, SB = SD. Gọi O là giao điểm của AC và BD.
a) Chứng minh rằng SO ⊥ mp(ABCD).
b) Gọi d là giao tuyến của mp(SAB) và mp(SCD), d1 là giao tuyến của mp(SBC) và mp(SAD). Chứng minh rằng SO ⊥ mp(d, d1).
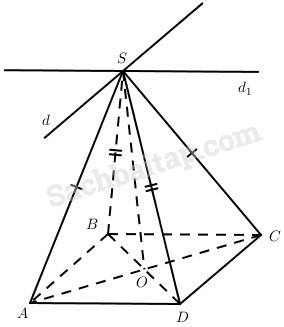
a) Vì ABCD là hình bình hành và \(O = AC \cap B{\rm{D}}\) nên OA = OC và OB = OD. Mặt khác SA = SC nên SO ⊥ AC và SB = SD nên SO ⊥BD.
Advertisements (Quảng cáo)
Vậy SO ⊥ mp(ABCD)
b) Vì AB // CD mà \(d = mp\left( {SAB} \right) \cap mp\left( {SC{\rm{D}}} \right)\) nên d //AB và d qua S.
Tương tự d1 //AD và d1 qua S.
Do \(SO \bot mp\left( {ABC{\rm{D}}} \right)\) nên \(SO \bot d,SO \bot {d_1}\) .
Vậy \(SO \bot mp\left( {d,{d_1}} \right)\).