Cho cấp số nhân. Câu 3.80 trang 99 sách bài tập Đại số và Giải tích 11 Nâng cao - Ôn tập chương III - Dãy số cấp số cộng và cấp số nhân
Cho cấp số nhân \(({u_n})\) có các hạng số khác 0 và
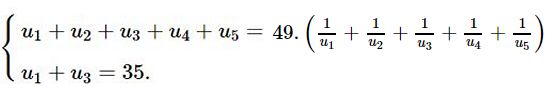
Hãy tìm \({u_1}.\)
- Gọi q là công bội của cấp số nhân \(({u_n})\), ta có \(q \ne 0\). Vì thế, \(({1 \over {{u_n}}})\) là một cấp số nhân với công bội \({1 \over q}.\)
Advertisements (Quảng cáo)
- Bằng phương pháp phản chứng, dễ dàng chứng minh được \(q \ne 1\). Do đó
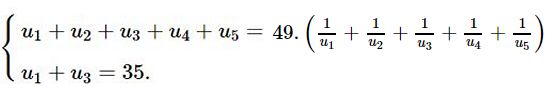
\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
{u_1}.{{1 - {q^5}} \over {1 - q}} = {{49} \over {{u_1}}} \cdot {{1 - {1 \over {{q^5}}}} \over {1 - {1 \over q}}} \hfill \cr
{u_1}\left( {1 + {q^2}} \right) = 35 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
u_1^2 = {{49} \over {{q^4}}} \hfill \cr
{u_1}\left( {1 + {q^2}} \right) = 35 \hfill \cr} \right. \cr} \)
Từ hệ (I) ta được \({u_1} = 28.\)