Trong mặt phẳng tọa độ, cho các đường thẳng \(({d_1})\) và \(({d_2})\) tương ứng vói đồ thị của các hàm số \(y = 2x - 1\) và \(y = x.\)
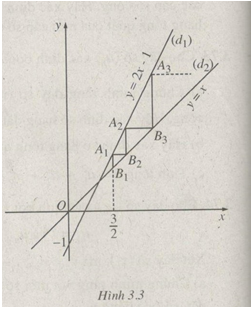
Xây dựng dãy các điểm \(({A_n})\) nằm trên \(({d_1})\) và dãy các điểm \(({B_n})\) nằm trên \(({d_2})\) theo cách sau (h.3.3):
\( \bullet \) \({A_1}\) và \({B_1}\) tương ứng là giao điểm của đường thẳng \(x = {3 \over 2}\) với \(({d_1})\) và \(({d_2})\);
\( \bullet \)Với mỗi số nguyên \(n \ge 2,{B_n}\) là giao điểm \(({d_2})\) với đường thẳng đi qua \({A_{n - 1}}\) và song song với trục hoành, \({A_n}\) là giao điểm của điểm \(({d_1})\) với đường đi qua \({B_n}\) và song song với trục tung.
Với mỗi số nguyên dương n, kí hiệu \({u_n}\) là hoành độ của \({A_n}\) và \({h_n}\) là độ dài của đoạn thẳng \({A_n}{B_n}\).
a) Chứng minh rằng dãy số \(({h_n})\) là một cấp số nhân. Hãy xác định số hạng đầu và công bội của cấp số nhân đó.
b) Dựa vào kết quả phần a), hãy xác định số hạng tổng quát của dãy số \(({u_n})\).

a ) Với mỗi \(n \ge 1,\) kí hiệu \({a_n}\) và \({b_n}\) tương ứng với tung độ của điểm \({A_n}\) và điểm \({B_n}.\) Khi đó :
Advertisements (Quảng cáo)
- Do \({A_n}\) nằm trên \(\left( {{d_1}} \right)\) nên \({a_n} = 2{u_n} - 1.\)
- Do \({B_n}\) là giao điểm của \(\left( {{d_2}} \right)\) và đường thẳng đi qua \({A_n}\), song song với trục tung \({b_n} = {u_n}\). Suy ra với mọi \(n \ge 1.\)
\({h_n} = {a_n} - {b_n} = \left( {2{u_n} - 1} \right) - {u_n} = {u_n} - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
Hơn nữa, với mỗi \(n \ge 1,\) do \({B_{n + 1}}\) nằm trên đường thẳng đi qua \({A_n}\) và song song với trục hoành nên \({b_{n + 1}} = {a_n} = 2{u_n} - 1\). Suy ra
\({u_{n + 1}} = 2{u_n} - 1\) với mỗi \(n \ge 1.\)
Từ đó ta được \({u_{n + 1}} - 1 = 2({u_n} - 1)\) với mọi \(n \ge 1,\) hay \({h_{n + 1}} = 2{h_n}\) với mọi \(n \ge 1\,\,\left( {theo\left( 1 \right)} \right).\) Vì thế, \(\left( {{h_n}} \right)\) là một cấp số nhân với số hạng đầu
\({h_1} = {u_1} - 1 = {3 \over 2} - 1 = {1 \over 2}\) và công bội \(q = 2\)
b) Ta có \({h_n} = {h_1}.{q^{n - 1}} = {1 \over 2} \times {2^{n - 1}} = {2^{n - 2}}\) với mọi \(n \ge 1.\) Suy ra
\({u_n} = {h_n} + 1 = {2^{n - 2}} + 1\) với mọi \(n \ge 1.\)
Baitapsgk.com
