Câu 30 trang 119 Sách bài tập Hình học 11 Nâng cao. Cho hình chóp S.ABDC có đáy là hình thoi cạnh a. cạnh bên SA vuông góc với mp(ABCD), SA = a và \(\widehat {ABC} = {60^0}\).. Bài 2 3 4: Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
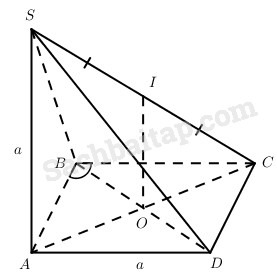
Cho hình chóp S.ABDC có đáy là hình thoi cạnh a. cạnh bên SA vuông góc với mp(ABCD), SA = a và \(\widehat {ABC} = {60^0}\).
a) Tính độ dài các cạnh SB, SC, SD.
b) Gọi I là trung điểm của SC. Chứng minh rằng IB = ID.

Advertisements (Quảng cáo)
a) Ta có \(SB = S{\rm{D}} = a\sqrt 2 ,AC = a\). (Vì ABC là tam giác cân mà \(\widehat {ABC} = {60^0}\))
Vậy \(SC = a\sqrt 2 \).
b) Gọi \(O = AC \cap B{\rm{D}}\) thì IO //SA nên \(I{\rm{O}} \bot \left( {ABC{\rm{D}}} \right)\), từ đó \(I{\rm{O}} \bot B{\rm{D}}\).
Mặt khác OB = OD nên BID là tam giác cân tại I, tức là IB = ID.
