Advertisements (Quảng cáo)
32. Trang 10 Sách bài tập Hình Học 11 nâng cao.
Chứng minh rằng:
a) Hợp thành của hai phép đối xứng trục có trục cắt nhau là một phép quay.
b) Mỗi phép quay đều có thể xem là hợp thành của hai phép đối xứng trục có trục cắt nhau, bằng nhiều cách.
c) Hợp thành của một số chẵn các phép đối xứng trục có các trục đối xứng đồng quy là một phép quay.
d) Hợp thành của một số lẻ các phép đối xứng trục có các trục đối xứng đồng quy là một phép đối xứng trục.
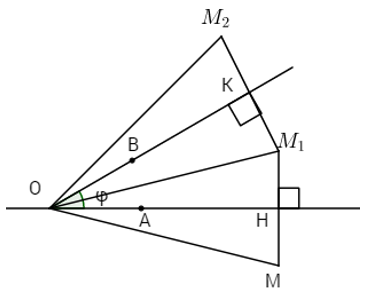
a) Giả sử cho hai phép đối xứng trục \({Đ_a}\) và \({Đ_b}\) có trục a và b cắt nhau tại O, còn F là hợp thành của \({Đ_a}\) và \({Đ_b}\). Lấy hai điểm A, B khác O lần lượt nằm trên a, b sao cho góc AOB không bù và đặt \(\varphi = \left( {OA,OB} \right).\)
(Chú ý rằng khi đó \(\left| \varphi \right| = \widehat {AOB}\) là góc hợp bởi hai đường thẳng a và b).
Với mọi điểm M khác O, giả sử \({Đ_a}\) biến M thành \({M_1}\) và \({Đ_b}\) biến \({M_1}\) thành \({M_2}\). Khi đó, nếu gọi H và K lần lượt là trung điểm của \(M{M_1}\) và \({M_1}{M_2}\) thì có:
Advertisements (Quảng cáo)
\(OM = O{M_1} = O{M_2}\)
Và \(\left( {OM,O{M_2}} \right) = \left( {OM,O{M_1}} \right) + \left( {O{M_1},O{M_2}} \right)\)
\(\eqalign{
& = 2\left( {OH,O{M_1}} \right) + 2\left( {O{M_1},OK} \right) \cr
& = 2\left( {OH,OK} \right) = 2\varphi \cr} \)
Vậy phép hợp thành F là phép quay tâm O góc quay \(2\varphi \)
b) Giả sử Q là phép quay tâm O góc quay \(\varphi .\) Ta lấy đường thẳng a nào đó đi qua O và b là ảnh của a qua phép quay tâm O góc quay \({\varphi \over 2}\) thì hợp thành của hai phép đối xứng trục \({Đ_a}\) và \({Đ_b}\) chính là phép quay Q (theo câu a). Cố nhiên có thể chọn a bằng nhiều cách khác nhau.
c) Nếu F là hợp thành của 2n phép đối xứng có trục đối xứng đồng quy tại O thì F là hợp thành của n phép quay có tâm O và do đó F là một phép quay.
d) Giả sử F là hợp thành của 2n + 1 phép đối xứng trục có các trục đều đi qua O. Gọi \({Đ_a}\) là phép đối xứng đầu tiên, thì 2n phép đối xứng trục còn lại có hợp thành là phép quay Q tâm O. Ta xem Q là hợp thành của hai phép đối xứng trục, trong đó phép thứ nhất là \({Đ_a}\) và phép thứ hai là \({Đ_b}\). Như vậy, F là hợp thành của ba phép đối xứng trục: \({Đ_a}\), \({Đ_a}\) và \({Đ_b}\). Vậy F chính là phép đối xứng trục \({Đ_b}\).