Cho hình vuông ABCD. Gọi S là điểm trong không gian sao cho SAB là tam giác đều và mp(SAB) vuông góc với mp(ABCD).
a) Chứng minh rằng \(mp\left( {SAB} \right) \bot mp\left( {SA{\rm{D}}} \right)\) và \(mp\left( {SAB} \right) \bot mp\left( {SBC} \right)\).
b) Tính góc giữa hai mặt phẳng (SAD) và (SBC).
c) Gọi H và I lần lượt là trung điểm của AB và BC. Chứng minh rằng
\(mp\left( {SHC} \right) \bot mp\left( {S{\rm{D}}I} \right)\).

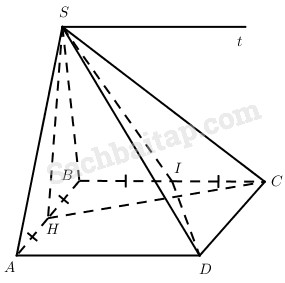
a) Gọi H là trung điểm của AB thì \(SH \bot AB\).
Advertisements (Quảng cáo)
Do \(\left( {SAB} \right) \bot \left( {ABC{\rm{D}}} \right)\) nên \(SH \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SH \bot A{\rm{D}}\), mặt khác \(A{\rm{D}} \bot AB\).
Vậy \(A{\rm{D}} \bot \left( {SAB} \right)\).
Từ đó \(\left( {SA{\rm{D}}} \right) \bot \left( {SAB} \right)\).
Tương tự như trên, ta có:
\(\left( {SBC} \right) \bot \left( {SAB} \right)\)
b) Giả sử \(\left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right) = St\), dễ thấy St // AD, từ đó \(mp\left( {ASB} \right) \bot St\). Do \(\widehat {ASB} = {60^0}\) nên góc giữa hai mặt phẳng (SAD) và (SBC) bằng 60°.
c) Vì ABCD là hình vuông; H, I lần lượt là trung điểm của AB và BC nên \(HC \bot DI\), mặt khác \(DI \bot SH\). Vậy \(DI \bot \left( {SHC} \right)\), từ đó \(\left( {S{\rm{D}}I} \right) \bot \left( {SHC} \right)\).
