Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, BC = 2a, cạnh bên SA vuông góc với mặt đáy, SA = a. Tính:
a) Các góc giữa các mặt phẳng chứa các mặt bên và mặt phẳng đáy của hình chóp.
b) Góc giữa hai mặt phẳng chứa hai mặt bên liên tiếp hoặc hai mặt bên đối diện của hình chóp.

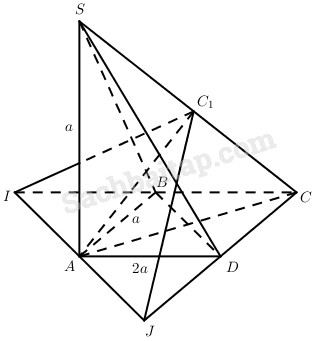
a) Dễ thấy
\(\eqalign{ & \left( {SAB} \right) \bot \left( {ABC{\rm{D}}} \right) \cr & \left( {SA{\rm{D}}} \right) \bot \left( {ABC{\rm{D}}} \right) \cr} \)
nên góc giữa mặt bên (SAB) và (SAD) với mp(ABCD) bằng 90°.
Ta có \(\left( {S{\rm{D}}A} \right) \bot C{\rm{D}}\) và SDA là tam giác vuông tại A nên \(\widehat {S{\rm{D}}A}\) là góc giữa hai mặt phẳng (SDC) và (ABCD).
Từ đó: \(\tan \widehat {S{\rm{D}}A} = {1 \over 2}\)
Tương tự, \(\tan \widehat {SBA} = 1 \Leftrightarrow \widehat {SBA} = {45^0}\).
Vậy mp(SCD) tạo với mp(ABCD) góc bằng φ mà \(\tan \varphi = {1 \over 2}\) và mp(SBC) tạo với mp(ABCD) góc 45°.
b) Vì \(\left( {SA{\rm{D}}} \right) \bot \left( {SAB} \right)\) nên góc giữa hai mặt phẳng đó bằng 90°.
Advertisements (Quảng cáo)
Ta cũng có \(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\) nên \(\left( {SC{\rm{D}}} \right) \bot SA{\rm{D}}\). Vậy góc giữa hai mặt phẳng (SAD) và (SCD) bằng 90°. Tương tự, ta cũng có góc giữa hai mặt phẳng (SAB) và (SBC) bằng 90°.
Ta cần phải tính góc giữa hai mặt phẳng (SBC) và (SDC).
Trong mp(ABCD), kẻ A qua đường thẳng vuông góc với AC, nó cắt hai đường thẳng BC và DC lần lượt tại I và J, thì \({\rm{IJ}} \bot {\rm{SC}}\).
Trong mp(SAC) kẻ \(A{C_1} \bot SC\) thì \(\left( {IJ{C_1}} \right) \bot SC\) .
Do đó, \(\widehat {I{C_1}J}\) hoặc \({180^0} - \widehat {I{C_1}J}\) là góc giữa hai mặt phẳng (SBC) và (SCD).
Ta có:
\(\eqalign{ & AJ = AC\tan \widehat {ACD} = 2a\sqrt 5 \cr & {1 \over {AC_1^2}} = {1 \over {A{S^2}}} + {1 \over {A{C^2}}} = {1 \over {{a^2}}} + {1 \over {5{a^2}}} = {6 \over {5{a^2}}} \cr & \Rightarrow A{C_1} = {{a\sqrt 5 } \over {\sqrt 6 }} \cr} \)
Đặt \(\widehat {A{C_1}J} = \alpha \) thì \(\tan \alpha = {{AJ} \over {A{C_1}}} = {{2a\sqrt 5 } \over {{{a\sqrt 5 } \over {\sqrt 6 }}}} = 2\sqrt 6 \)
Đặt \(\widehat {A{C_1}I} = \beta \) thì \(\tan \beta = {{AI} \over {A{C_1}}} = {{AC\tan \widehat {ACI}} \over {A{C_1}}} = {{a\sqrt 5 .{1 \over 2}} \over {{{a\sqrt 5 } \over {\sqrt 6 }}}} = {{\sqrt 6 } \over 2}\)
Đặt \(\widehat {I{C_1}J} = \varphi \) thì \(\tan \varphi = {{2\sqrt 6 + {{\sqrt 6 } \over 2}} \over {1 - 2\sqrt 6 .{{\sqrt 6 } \over 2}}} = - {{\sqrt 6 } \over 2}\)
Vậy góc giữa mp(SBC) và (SCD) là \({180^0} - \varphi \) mà \(\tan \varphi = {{ - \sqrt 6 } \over 2}\).
