Chứng minh rằng hai hình thang ấy bằng nhau nếu AB = A’B’, BC = B’C’ và CD = C’D’.. Câu 48 trang 12 Sách bài tập Hình Học 11 Nâng cao - Bài 5: Hai hình bằng nhau
48. Trang 12 Sách bài tập Hình Học 11 Nâng cao
Cho hình thanh ABCD vuông tại A và D, hình thang A’B’C’D’ vuông góc tại A’ và D’.
Chứng minh rằng hai hình thang ấy bằng nhau nếu AB = A’B’, BC = B’C’ và CD = C’D’.
(h.28)
Advertisements (Quảng cáo)
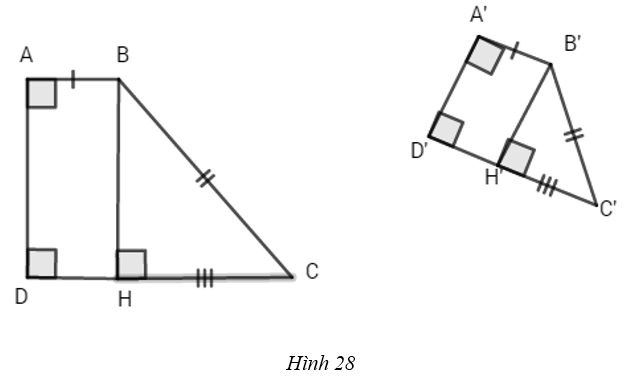
Nếu AB = CD thì kết quả là hiển nhiên.
Giả sử AB < CD, kẻ BH\(\bot\) CD, B’H’ \(\bot\) C’D’
Ta có CH = CD – AB = C’D’ - A’B’ = C’H’.
Từ đó, suy ra hai tam giác vuông BHC và B’H’C’ bằng nhau. Gọi F là phép dời hình biến tam giác BHC thành tam giác B’H’C’, thì dễ thấy rằng F biến A thành A’ và biến D thành D’. Do đó F biến hình thang ABCD thành hình thang A’B’C’D’. Vậy hai hình thang đó bằng nhau.