49. Trang 12 Sách bài tập Hình Học 11 Nâng cao
Chứng minh rằng hai tam giác bằng nhau nếu có các đường tròn nội tiếp bằng nhau, một cặp đường tròn bàng tiếp bằng nhau, đồng thời khoảng cách giữa tâm đường tròn nội tiếp và bàng tiếp của hai tam giác đó cũng bằng nhau.

(h.29)
Advertisements (Quảng cáo)
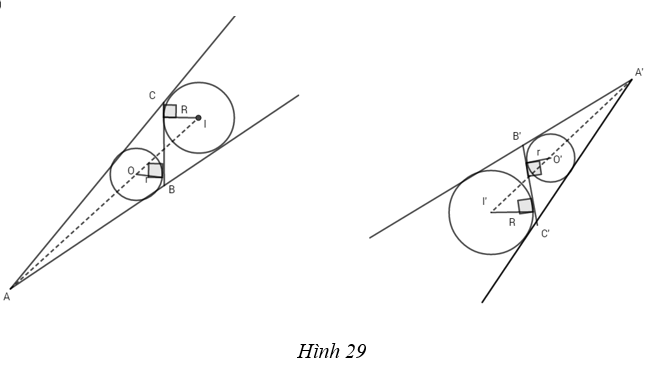
Giả sử tam giác ABC có đường tròn nội tiếp (O;r), đường tròn bàng tiếp góc A là (I; R), tam giác A’B’C’ có đường tròn nội tiếp (O’; r), đường tròn bàng tiếp góc A’ là (I’; R); đồng thời OI = O’I’.
Vì OI = O’I’ nên có phép dời hình F biến O thành O’ và I thành I’, khi đó F biến (O; r) thành (O’; r) và biến (I; R) thành (I’; R). Mặt khác F biến cặp tiếp tuyến chung ngoài AB và AC của hai đường tròn (O) và (I) thành cặp tiếp tuyến chung ngoài A’B’ và A’C’ (hoặc thành A’C’ và A’B’), còn tiếp tuyến chung BC phải biến thành tiếp tuyến chung B’C’.
Suy ra F biến tam giác ABC thành tam giác A’B’C’ hoặc thành tam giác A’C’B’, tức là hai tam giác ABC và A’B’C’ bằng nhau.
