Chứng minh rằng nếu ba trung tuyến của tam giác ABC lần lượt bằng ba trung tuyến của tam giác A’B’C’ thì hai tam giác đó bằng nhau.. Câu 51 trang 13 Sách bài tập Hình Học 11 Nâng cao - Bài 5: Hai hình bằng nhau
51. Trang 13 Sách bài tập Hình Học 11 Nâng cao
Chứng minh rằng nếu ba trung tuyến của tam giác ABC lần lượt bằng ba trung tuyến của tam giác A’B’C’ thì hai tam giác đó bằng nhau.
(h.31)
Advertisements (Quảng cáo)
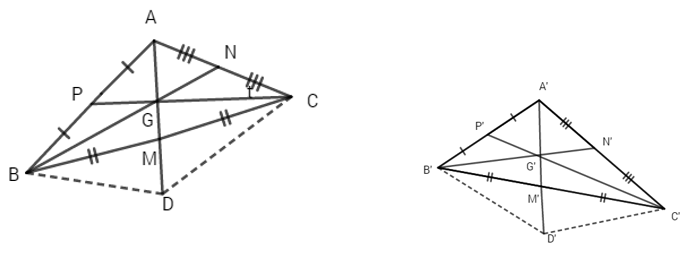
Giả sử tam giác ABC có ba trung tuyến AM, BN, CP cắt nhau tại G; tam giác A’B’C’ có ba trung tuyến A’M’, B’N’, C’P’ cắt nhau tại G’ và AM = A’M’, BN = B’N’, CP = C’P’ .
Ta lấy điểm D và D’ sao cho BGCD và B’G’C’D’ là những hình bình hành. Dễ thấy rằng hai tam giác GCD và G’C’D’ bằng nhau. Bởi vậy, có một phép dời hình F biến G, C, D lần lượt thành G’, C’, D’. Rõ ràng khi đó F biến A thành A’, B thành B’ nên hai tam giác ABC và A’B’C’ bằng nhau.