Chứng minh rằng có phép vị tự biến tam giác này thành tam giác kia.. Câu 53 trang 14 Sách bài tập Hình Học 11 Nâng cao - Bài 6 7: Phép vị tự. Phép đồng dạng
53. Trang 14 Sách bài tập Hình Học 11 Nâng cao
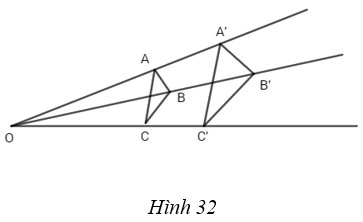
Cho hai tam giác ABC và A’B’C’ không bằng nhau nhưng có các cạnh tương ứng song song: AB // A’B’, BC // B’C’ và CA // C’A’. Chứng minh rằng có phép vị tự biến tam giác này thành tam giác kia.

(h.32)
Advertisements (Quảng cáo)
Vì AB và A’B’ song song nhưng không bằng nhau nên hai đường thẳng AA’ và BB’ cắt nhau tại điểm O. Gọi V là phép vị tự tâm O tỉ số
\(k = {{OA’} \over {OA}}\)
Thì V biến điểm C thành điểm C1 sao cho:
\(A'{C_1}//AC;\,B'{C_1}\,//BC.\)
Suy ra C1 trùng với C’, tức là V cũng biến C thành C’. Vậy ta có điều phải chứng minh.
