54. Trang 14 Sách bài tập Hình Học 11 Nâng cao
Cho hai phép vị tự V1 có tâm O1 tỉ số k1 và V2 có tâm O2 tỉ số k2. Gọi F là hợp thành của V1 và V2. Chứng minh rằng:
a) F là một phép tịnh tiến nếu k1k2 = 1. Hãy xác định vec tơ tịnh tiến.
b) F là một phép vị tự nếu k1k2 1. Hãy xác định tâm và tỉ số của phép vị tự đó.
Giải
Lấy một điểm M bất kỳ, nếu V1 biến M thành M1 và V2 biến M1 thành M2 thì \(\overrightarrow {{O_1}{M_1}} = {k_1}\overrightarrow {{O_1}M} \) và \(\overrightarrow {{O_2}{M_2}} = {k_2}\overrightarrow {{O_2}{M_1}} \).
Khi đó, phép hợp thành F biến M thành M2. Gọi I là ảnh của O1 qua phép vị tự V2, tức là \(\overrightarrow {{O_2}I} = {k_2}\overrightarrow {{O_2}{O_1}} \).
Khi đó \(\overrightarrow {I{M_2}} = {k_2}\overrightarrow {{O_1}{M_1}} = {k_1}{k_2}\overrightarrow {{O_1}M} \).
a) (h.33)
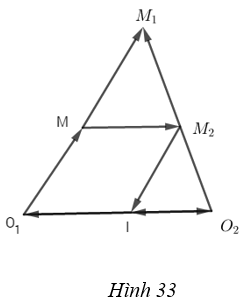
Nếu k1k2 = 1 thì \(\overrightarrow {I{M_2}} = \overrightarrow {{O_1}M} \) nên \(\overrightarrow {M{M_2}} = \overrightarrow {{O_1}I} = \overrightarrow {{O_1}{O_2}} + \overrightarrow {{O_2}I} = \left( {1 - {k_2}} \right)\overrightarrow {{O_1}{O_2}} \).
Vậy trong trường hợp này F là phép tịnh tiến vectơ \(\overrightarrow u = \left( {1 - {k_2}} \right)\overrightarrow {{O_1}{O_2}} \).
b) (h.34)
Advertisements (Quảng cáo)
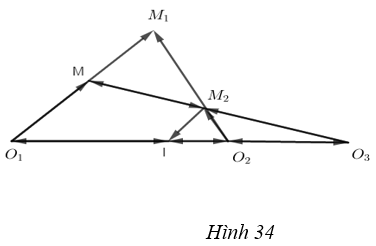
Nếu k1k2 \(\ne\) 1 ta chọn điểm O3 sao cho \(\overrightarrow {{O_3}I} = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} \)
Khi đó \(\overrightarrow {{O_3}{M_2}} = \overrightarrow {{O_3}I} + \overrightarrow {I{M_2}} \)
\( = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} + {k_1}{k_2}\overrightarrow {{O_1}M} \)
\( = {k_1}{k_2}\overrightarrow {{O_3}M} \)
Vậy F là phép vị tự tâm O3 tỉ số \({k_1}{k_2}\).
Chú ý rằng tâm O3 của phép vị tự đó được xác định bởi đẳng thức:
\(\overrightarrow {{O_3}I} = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} \)
Hay \(\overrightarrow {{O_3}{O_1}} + \overrightarrow {{O_1}{O_2}} + \overrightarrow {{O_2}I} = {k_1}{k_2}\overrightarrow {{O_3}{O_1}} \).
Suy ra: \(\overrightarrow {{O_1}{O_2}} + {k_2}\overrightarrow {{O_2}{O_1}} = \left( {1 - {k_1}{k_2}} \right)\overrightarrow {{O_1}{O_3}} \).
Do đó: \(\overrightarrow {{O_1}{O_3}} = {{1 - {k_2}} \over {1 - {k_1}{k_2}}}\overrightarrow {{O_1}{O_2}} \).
Cũng chú ý rằng tâm của ba phép vị tự V1, V2 và F là ba điểm thẳng hàng O1, O2 và O3.
