56. Trang 14 Sách bài tập Hình Học 11 Nâng cao
Cho hai đường tròn \(\left( {{O_1}} \right),\left( {{O_2}} \right)\) ngoài nhau và không bằng nhau. Một đường tròn (O) thay đổi tiếp xúc ngoài với \(\left( {{O_1}} \right)\) và \(\left( {{O_2}} \right)\). Gọi các tiếp điểm tương ứng là A và B. Chứng minh rằng đường thẳng AB luôn luôn đi qua một điểm cố định. Nếu thay giả thiết “tiếp xúc ngoài” bằng “tiếp xúc trong” thì kết quả trên sẽ thay đổi như thế nào?

(h.35)
Advertisements (Quảng cáo)
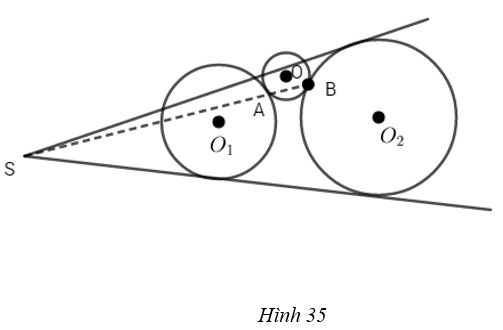
Điểm A là tâm vị tự trong của \(\left( {{O_1}} \right)\) và (O), B là tâm vị tự trong của (O) và \(\left( {{O_2}} \right)\). Nếu gọi S là tâm vị tự ngoài của \(\left( {{O_1}} \right)\) và \(\left( {{O_2}} \right)\) thì theo bài tập 55, đường thẳng AB đi qua S.
Nếu thay “tiếp xúc ngoài” bằng “tiếp xúc trong”, đường thẳng AB cũng đi qua S. (Chứng minh tương tự như trường hợp tiếp xúc ngoài).
