Câu 57 trang 125 Sách bài tập Hình học 11 Nâng cao. \(\eqalign{ & M{N^2} = N{H^2} + H{M^2} \cr & = {{S{A^2}} \over 4} + {{B{C^2}} \over 4} = {1 \over 4}\left( {{h^2} + {b^2}} \right) \cr . Bài 5: Khoảng cách
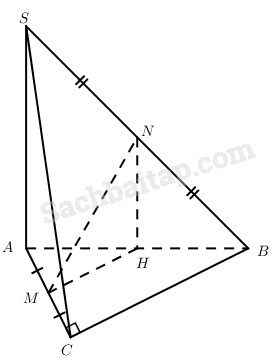
Cho hình chóp S.ABC có đáy là tam giác vuông ở C, cạnh SA vuông góc với mặt phẳng đáy, \(AC = a,BC = b,SA = h\). Gọi M và N lần lượt là trung điểm của các cạnh AC và SB.
a) Tính độ dài MN.
b) Tìm hệ thức liên hệ giữa a, b, h để MN là đường vuông góc chung của AC và SB.
Advertisements (Quảng cáo)
a) Gọi H là trung điểm của AB thì NH // SA.
Do \(SA \bot \left( {ABC} \right)\) nên \(NH \bot \left( {ABC} \right)\), từ đó \(\widehat {NHM} = {90^0}\). Vậy
\(\eqalign{ & M{N^2} = N{H^2} + H{M^2} \cr & = {{S{A^2}} \over 4} + {{B{C^2}} \over 4} = {1 \over 4}\left( {{h^2} + {b^2}} \right) \cr & \Rightarrow MN = {1 \over 2}\sqrt {{h^2} + {b^2}} \cr} \)
b) h = b