Câu 68 trang 16 Sách bài tập Hình học 11 Nâng cao. Ôn tập chương I - Phép dời hình và phép đồng dạng
Cho hai đoạn thẳng bằng nhau AB và A’B; (AB = A’B;). Chứng minh rằng có một phép đối xứng trượt biến A thành A’, biến B thành B’.
Advertisements (Quảng cáo)
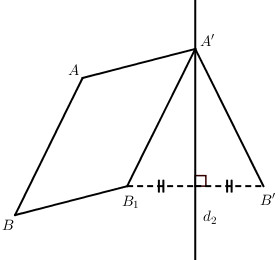
Gọi T là phép tịnh tiến theo vectơ \(\overrightarrow v = \overrightarrow {AA’} \) . Khi đó T biến A thành A’ và biến B thành B1. Gọi d2 là đường trung trực của đoạn thẳng B1B’ nếu B1 khác B’, còn nếu B1 trùng B’ thì lấy d2 là đường thẳng A’B’. Hiển nhiên khi đó d2 đi qua A’ và phép đối xứng Đ2 qua đường thẳng d2 biến A’ thành A’ và biến B1 thành B’. Vậy hợp thành F của T và Đ2 sẽ biến A thành A’ và biến B thành B’. Suy ra F là phép đối xứng trượt.