Cho hình lăng trụ tam giác ABC.A’B’C’. Lấy các điểm \({A_1},{B_1},{C_1}\) lần lượt thuộc các cạnh bên AA’, BB’, CC’ sao cho \({{A{A_1}} \over {AA’}} = {{B'{B_1}} \over {BB’}} = {{C'{C_1}} \over {CC’}} = {3 \over 4}\). Trên các đoạn thẳng CA1 và A’B1 lần lượt lấy các điểm I, J sao cho IJ // B’C1. Tính tỉ số \({{IJ} \over {B'{C_1}}}\) .

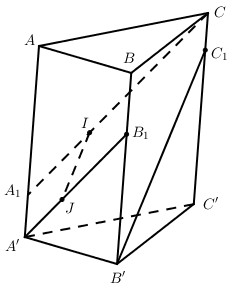
Đặt \(\overrightarrow {AA’} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \). Theo giả thiết ta có:
\(\overrightarrow {A{A_1}} = {3 \over 4}\overrightarrow a ,\overrightarrow {B'{B_1}} = - {3 \over 4}\overrightarrow a ,\overrightarrow {C'{C_1}} = - {3 \over 4}\overrightarrow a .\)
Ta có:
\(\eqalign{ & \overrightarrow {C{A_1}} = \overrightarrow {CA} + \overrightarrow {A{A_1}} \cr & = {3 \over 4}\overrightarrow a - \overrightarrow c ; \cr & \overrightarrow {A'{B_1}} = \overrightarrow {A’B’} + \overrightarrow {B'{B_1}} \cr & = - {3 \over 4}\overrightarrow a + \overrightarrow b ; \cr & \overrightarrow {B'{C_1}} = \overrightarrow {B’A’} + \overrightarrow {A’C’} + \overrightarrow {C'{C_1}} \cr & = - {3 \over 4}\overrightarrow a - \overrightarrow b + \overrightarrow c \cr} \)
Vì I thuộc CA1 nên \(\overrightarrow {CI} = t\overrightarrow {C{A_1}} = {3 \over 4}t\overrightarrow a - t\overrightarrow c .\)
Do J thuộc A’B1 nên \(\overrightarrow {A’J} = m\overrightarrow {A'{B_1}} = - {3 \over 4}m\overrightarrow a + m\overrightarrow b \) .
Advertisements (Quảng cáo)
Mặt khác
\(\eqalign{ & \overrightarrow {IJ} = \overrightarrow {IC} + \overrightarrow {CA’} + \overrightarrow {A’J} \cr & = - {3 \over 4}t\overrightarrow a + t\overrightarrow c + \overrightarrow a - \overrightarrow c - {3 \over 4}m\overrightarrow a + m\overrightarrow b \cr & = \left( {1 - {3 \over 4}t - {3 \over 4}m} \right)\overrightarrow a + m\overrightarrow b + \left( {t - 1} \right)\overrightarrow c \cr} \)
Ta có:
\(\eqalign{ & IJ//B'{C_1} \Leftrightarrow \overrightarrow {IJ} = k\overrightarrow {B'{C_1}} \cr & \Leftrightarrow \left\{ \matrix{ 1 - {3 \over 4}t - {3 \over 4}m = - {3 \over 4}k \hfill \cr m = - k \hfill \cr t - 1 = k \hfill \cr} \right. \cr} \)
Suy ra
\(\eqalign{ & 1 - {3 \over 4}\left( {k + 1} \right) + {3 \over 4}k = - {3 \over 4}k \cr & \Leftrightarrow {1 \over 4} + {3 \over 4}k = 0 \Leftrightarrow k = - {1 \over 3} \cr & \Rightarrow t = {2 \over 3},m = {1 \over 3}. \cr} \)
Vậy điểm I thuộc A1C được xác định bởi \(\overrightarrow {CI} = {2 \over 3}\overrightarrow {C{A_1}} \) và J thuộc A’B1 được xác định \(\overrightarrow {A’J} = {1 \over 3}\overrightarrow {A'{B_1}} \).
Khi đó, ta có \({{IJ} \over {B'{C_1}}} = {1 \over 3}.\)
