Cho M, N lần lượt là trung điểm của các cạnh AB và CD của tứ diện ABCD; P là điểm thuộc đường thẳng AD sao cho \(\overrightarrow {PA} = k\overrightarrow {P{\rm{D}}} \), k là số cho trước (k ≠ 1). Xác định điểm Q thuộc đường thẳng BC sao cho PQ và MN cắt nhau. Khi đó, hãy tính tỉ số \({{QB} \over {QC}}.\)

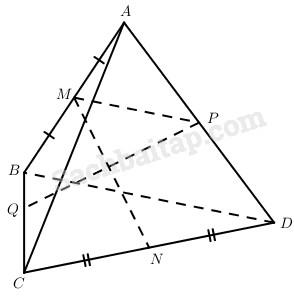
MN cắt PQ nên các điểm M, N, P, Q cùng thuộc một mặt phẳng. Điều này tương đương với có các số x, y sao cho \(\overrightarrow {MP} = x\overrightarrow {MN} + y\overrightarrow {MQ} \).
Đặt \(\overrightarrow {DA} = \overrightarrow a ,\overrightarrow {DB} = \overrightarrow b ,\overrightarrow {DC} = \overrightarrow c .\)
Khi đó
Advertisements (Quảng cáo)
\(\eqalign{ & \overrightarrow {MN} = {1 \over 2}\left( {\overrightarrow {A{\rm{D}}} + \overrightarrow {BC} } \right) \cr & = {1 \over 2}\left( { - \overrightarrow a - \overrightarrow b + \overrightarrow c } \right) \cr & \overrightarrow {MP} = {{\overrightarrow {MA} - k\overrightarrow {M{\rm{D}}} } \over {1 - k}} \cr & = {1 \over {1 - k}}\left[ {{1 \over 2}\left( {\overrightarrow a - \overrightarrow b } \right) - {k \over 2}\left( {\overrightarrow a - \overrightarrow b - 2\overrightarrow a } \right)} \right] \cr & = {1 \over {1 - k}}\left[ {{1 \over 2}\left( {\overrightarrow a - \overrightarrow b } \right) + {k \over 2}\left( {\overrightarrow a + \overrightarrow b } \right)} \right] \cr & = {1 \over {2\left( {1 - k} \right)}}\left[ {\left( {1 + k} \right)\overrightarrow a + \left( {k - 1} \right)\overrightarrow b } \right] \cr & = {{k + 1} \over {2\left( {1 - k} \right)}}\overrightarrow a - {1 \over 2}\overrightarrow {b.} \cr & \overrightarrow {MQ} = \overrightarrow {MB} + \overrightarrow {BQ} \cr & = {1 \over 2}\left( {\overrightarrow b - \overrightarrow a } \right) + t\left( { - \overrightarrow b + \overrightarrow c } \right) \cr & = - {1 \over 2}\overrightarrow a + \left( {{1 \over 2} - t} \right)\overrightarrow b + t\overrightarrow c \cr} \)
Từ đó ta có
\(\eqalign{ & \overrightarrow {MP} = x\overrightarrow {MN} + y\overrightarrow {MQ} \cr & \Leftrightarrow \left\{ \matrix{ {{k + 1} \over {2\left( {1 - k} \right)}} = - {1 \over 2}x - {1 \over 2}y \hfill \cr - {1 \over 2} = - {1 \over 2}x + y\left( {{1 \over 2} - t} \right) \hfill \cr 0 = {1 \over 2}x + yt \hfill \cr} \right. \cr & \Rightarrow y = - 1,x = {{k + 1} \over {k - 1}} + 1 = {{2k} \over {k - 1}} \cr & t = {k \over {k - 1}} \cr} \)
Như vậy
\(\eqalign{ & \overrightarrow {BQ} = {k \over {k - 1}}\overrightarrow {BC} = {k \over {k - 1}}\left( {\overrightarrow {BQ} + \overrightarrow {QC} } \right) \cr & \Leftrightarrow \left( {1 - {k \over {k - 1}}} \right)\overrightarrow {BQ} = {k \over {k - 1}}\overrightarrow {QC} \cr & \Leftrightarrow - \overrightarrow {BQ} = k.\overrightarrow {QC} \cr & \Leftrightarrow {{QB} \over {QC}} = \left| k \right| \cr} \)
