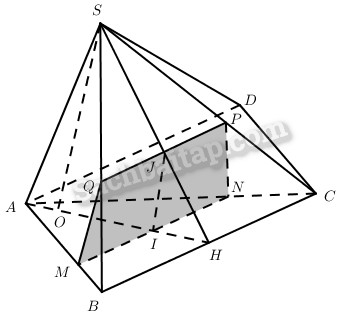
Cho tam giác đề ABC có chiều cao AH = 5a. Điểm O thuộc đoạn thẳng AH sao cho AO = a. Điểm S trên đường thẳng vuông góc với mặt phẳng (ABC) tại O và SO = 2a.
a) Chứng minh AS và CS vuông góc với nhau. Tính góc giữa hai đường thẳng AB và SC.
b) Gọi I là trung điểm của OH; (α) là mặt phẳng đi qua điểm I và vuông góc với AH. Thiết diện của hình chóp S.ABC khi cắt bởi (α) là hình gì? Tính diện tích thiết diện.

a) Dễ thấy
\(\eqalign{ & BC = {{10{\rm{a}}} \over {\sqrt 3 }} \cr & S{A^2} = S{O^2} + A{O^2} \cr & = 4{{\rm{a}}^2} + {a^2} = 5{{\rm{a}}^2} \cr & S{C^2} = S{O^2} + A{O^2} \cr & = 4{{\rm{a}}^2} + 16{{\rm{a}}^2} + {{25{{\rm{a}}^2}} \over 3} \cr & = {{85{a^2}} \over 3} \cr & A{C^2} = {{100{{\rm{a}}^2}} \over 3} \cr} \)
Ta có \(S{A^2} + S{C^2} = A{C^2}\)
Vậy \(SA \bot SC\).
+ Kẻ AD song song và bằng BC (hai tia AD, BC cùng chiều) thì góc giữa AB và SC chính là góc giữa CD và SC, đó là \(\widehat {SC{\rm{D}}}\) hoặc \({180^0} - \widehat {SC{\rm{D}}}\).
Dễ thấy \(SA \bot BC\), do AD // BC nên \(SA \bot A{\rm{D}}\), tức là tam giác SAD vuông.
Do đó \(S{{\rm{D}}^2} = S{A^2} + A{{\rm{D}}^2} = 5{{\rm{a}}^2} + {{100{{\rm{a}}^2}} \over 3} = {{115{{\rm{a}}^2}} \over 3}\),
mặt khác \(S{{\rm{D}}^2} = S{C^2} + D{C^2} - 2{\rm{S}}C.DC\cos \widehat {SCD}\)
Advertisements (Quảng cáo)
nên ta có
\(\eqalign{& {{115{{\rm{a}}^2}} \over 3} \cr & = {{85{{\rm{a}}^2}} \over 3} + {{100{{\rm{a}}^2}} \over 3} - 2.{{a\sqrt {85} } \over {\sqrt 3 }}.{{10{\rm{a}}} \over {\sqrt 3 }}\cos \widehat {SCD} \cr & \Rightarrow \cos \widehat {SCD} = {7 \over {2\sqrt {85} }} \cr} \)
Vậy góc giữa AB và SC là α mà
\(\cos \alpha = {7 \over {2\sqrt {85} }}\).
Do \(\left( \alpha \right) \bot AH,SO \bot AH\) và \(BC \bot AH\) nên SO và BC cùng song song với (α). Khi đó \(\left( \alpha \right) \cap \left( {ABC} \right) = MN\), MN qua I và MN // BC
\(\eqalign{ & \left( \alpha \right) \cap \left( {SOH} \right) = IJ,IJ//SO \cr & \left( \alpha \right) \cap \left( {SBC} \right) = PQ \cr} \)
PQ qua J và PQ // BC.
Dễ thấy MNPQ là hình thang cân với chiều cao JI.
Ta có :
\(\eqalign{ & {\rm{IJ}} = {1 \over 2}SO = a \cr & PQ = {1 \over 2}BC = {{5{\rm{a}}} \over {\sqrt 3 }} \cr & {{MN} \over {BC}} = {{3{\rm{a}}} \over {5{\rm{a}}}} \Rightarrow MN = {{10{\rm{a}}.3} \over {\sqrt 3 .5}} = 2{\rm{a}}\sqrt 3 . \cr} \)
Suy ra
\(\eqalign{ & {S_{MNPQ}} = {1 \over 2}\left( {MN + PQ} \right).{\rm{IJ}} \cr & = {1 \over 2}\left( {2{\rm{a}}\sqrt 3 + {{5{\rm{a}}} \over {\sqrt 3 }}} \right).a = {{11{{\rm{a}}^2}} \over {2\sqrt 3 }} \cr} \)
