Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B. AB = c, BC = a cạnh bên AA’ = h, trong đó \({h^2} > {a^2} + {c^2}\). Một mặt phẳng (P) đi qua điểm A và vuông góc với CA’
a) Xác định thiết diện cùa hình lăng trụ khi cắt bởi mp(P).
b) Tính diện tích thiết diện.

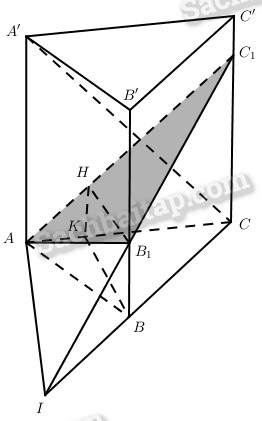
a) (P) cắt (ACC’A’) theo giao tuyến đi qua A và vuông góc với A’C.
Do \(AA’ = h > AC = \sqrt {{a^2} + {c^2}} \) nên giao tuyến đó cắt CC’ tại C1, C1 thuộc cạnh CC’. Mặt khác (P) cắt (ABC) theo giao tuyến vuông góc với A’C, tức là giao tuyến đó vuông góc với AC, giao tuyến này cắt BC tại I. Khi đó IC1 cắt BB’ tại B1. Thiết diện là tam giác AB1C1.
b) Tính diện tích thiết diện
Dễ thấy \(\varphi = \widehat {CA{C_1}}\) là góc giữa (P) và (ABC), ngoài ra \(\widehat {{C_1}AC} = \widehat {AA’C}\)
Advertisements (Quảng cáo)
\(\cos \varphi = {h \over {\sqrt {{a^2} + {c^2} + {h^2}} }}\)
Ta có
\(\eqalign{ & {S_{ABC}} = {S_{A{B_1}{C_1}}}\cos \varphi \cr & \Rightarrow {S_{A{B_1}{C_1}}} = {{{S_{ABC}}} \over {\cos \varphi }} = {{ac} \over {2h}}\sqrt {{a^2} + {c^2} + {h^2}} \cr} \).
Chú ý: Có thể tính \({S_{A{B_1}{C_1}}}\) bằng cách tính AC1 và đường cao B1H của tam giác đó. Dễ thấy B1H song song với BK, trong đó \(BK \bot AC\) vì B1H và BK cùng vuông góc với (ACC’A’)
Ngoài ra \({B_1}H = BK = {{ac} \over {\sqrt {{a^2} + {c^2}} }}\)
∆AA’C đồng dạng ∆ACC1
\( \Rightarrow A{C_1} = {{A’C.AC} \over {AA’}} = {{\sqrt {{a^2} + {c^2} + {h^2}} .\sqrt {{a^2} + {c^2}} } \over h}\).
Từ đó tính được diện tích tam giác AB1C1
