Cho hình chóp đều S.ABCD cạnh đáy bằng a.
a) Tính góc tạo bởi mặt phẳng chứa mặt bên và mặt đáy. Tính góc tạo bởi hai mặt phẳng chứa hai mặt bên liên tiếp nếu chiều cao hình chóp bằng a.
b) Xét mặt phẳng (P) đi qua điểm A, song song với CD và vuông góc với mp(SCD), chia tam giác SCD thành hai phần với tỉ số diện tích bằng \({1 \over 8}\) (phần thứ nhất chứa đỉnh). Tính diện tích thiết diện của hình chóp khi cắt bời mặt phẳng (P).

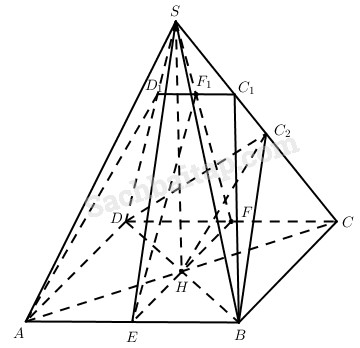
a) ● Gọi E là trung điểm của AB và H là tâm của hình vuông ABCD. Khi ấy SHE là tam giác vuông tại H và \(AB \bot \left( {SHE} \right)\). Vậy góc giữa mặt phẳng (SAB) và mặt phẳng đáy (ABCD) là \(\widehat {SEH}\).
Đặt \(\widehat {SEH} = \alpha \) thì \(\tan \alpha = {{2h} \over a}\left( {SH = h} \right)\).
Tương tự như trên ta có góc giữa các mặt phẳng chứa mỗi mặt bên còn lại của hình chóp với mặt phẳng đáy (ABCD) cũng bằng α và \(\tan \alpha = {{2h} \over a}\).
● Khi h = a thì góc tạo bởi mỗi mặt phẳng chứa mặt bên và mặt phẳng đáy bằng α và tanα = 2.
Kẻ \(H{C_2} \bot SC\) thì ta có \(mp\left( {B{C_2}D} \right) \bot SC\).
Vậy góc giữa mp(SBC) và mp(SDC) bằng \(\widehat {B{C_2}D}\) hoặc \({180^0} - \widehat {B{C_2}D}\).
Ta tính \(\widehat {B{C_2}D}\)
Dễ thấy
\(\eqalign{ & H{C_2} = {{HC.H{\rm{S}}} \over {SC}} \cr & = {{{{a\sqrt 2 } \over 2}.{\rm{a}}} \over {\sqrt {{{2{{\rm{a}}^2}} \over 4} + {a^2}} }} = {{a\sqrt 2 } \over {\sqrt 6 }} = {a \over {\sqrt 3 }} \cr} \)
Từ đó
\(\eqalign{ & BC_2^2 = H{B^2} + HC_2^2 \cr & = {{{a^2}} \over 2} + {{{a^2}} \over 3} = {{5{{\rm{a}}^2}} \over 6} \cr} \)
Đặt \(\beta = \widehat {B{C_2}D}\) thì
\(\eqalign{ & B{{\rm{D}}^2} = BC_2^2 + DC_2^2 - 2B{C_2}.D{C_2}\cos \beta \cr & \Leftrightarrow 2{a^2} = {{5{a^2}} \over 6} + {{5{a^2}} \over 6} - 2.{{5{a^2}} \over 6}\cos \beta \cr & = 2.{{5{a^2}} \over 6}\left( {1 - \cos \beta } \right) \cr & \Leftrightarrow 1 = {5 \over 6}\left( {1 - \cos \beta } \right) \Rightarrow \cos \beta = 1 - {6 \over 5} = - {1 \over 5} \cr} \)
Advertisements (Quảng cáo)
Vậy góc giữa mp(SBC) và mp(SCD) là \({180^0} - \beta \) mà \(\cos \beta = - {1 \over 5}\).
Tương tự như trên, ta có góc giữa hai mặt chứa hai bên mặt bên liên tiếp cũng được xác định bởi β mà \(\cos \beta = - {1 \over 5}\) .
b) Vì (P) đi qua A và song song với CD nên (P) chứa cạnh AB. Do (P) vuông góc với (SCD) nên (P) chứa EF1 vuông góc với mặt phẳng (SCD). Dễ thấy F1 thuộc SF, trong đó F là trung điểm của CD.
Mặt khác (P) chia tam giác SCD thành hai phần mà tỉ số diện tích hai phần bằng \({1 \over 8}\) nên \({{S{F_1}} \over {SF}} = {1 \over 3}\).
Khi ấy thiết diện của hình chóp S.ABCD cắt bới (P) là hình thang cân ABC1D1 mà \({C_1}{D_1} = {1 \over 3}C{\rm{D}} = {a \over 3}\) với đường cao EF1.
Ta có
\(\eqalign{ & {S_{AB{C_1}{D_1}}} = {1 \over 2}\left( {AB + {C_1}{D_1}} \right).E{F_1} \cr & = {1 \over 2}\left( {a + {a \over 3}} \right)E{F_1} = {{2a} \over 3}.E{F_1} \cr} \)
Ta tính EF1
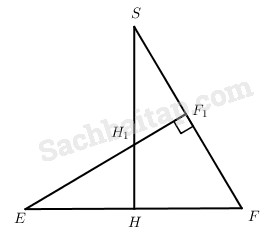
Vì \(S{H_1}.SH = S{F_1}.SF = {1 \over 3}S{F^2}\)
nên \({{S{H_1}} \over {SH}} = {1 \over 3}.{{S{F^2}} \over {S{H^2}}}\)
Mặt khác \(HE = HF,S{F_1} = {1 \over 2}{F_1}F\)
nên dễ thấy \({{S{H_1}} \over {SH}} = {1 \over 2}\),
từ đó \({{S{H^2}} \over {S{F^2}}} = {2 \over 3} \Rightarrow {{SH} \over {SF}} = {{\sqrt 6 } \over 3}\).
Ta lại có \({{SH} \over {SF}} = \sin \widehat {SFH} = {{E{F_1}} \over {EF}} = {{E{F_1}} \over a}\).
Vậy \(E{F_1} = {{a\sqrt 6 } \over 3}\).
Từ đó \({S_{AB{C_1}{D_1}}} = {{2{\rm{a}}} \over 3}.{{a\sqrt 6 } \over 3} = {{2{{\rm{a}}^2}\sqrt 6 } \over 9}\).
