
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) \( \bot \) (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.

- Hai mặt phẳng vuông góc, nếu có một đường thẳng trong mặt phẳng này vuông góc vào giao tuyến 2 mặt phẳng thì đường thẳng đó vuông góc với mặt phẳng còn lại.
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
- Nếu đường vuông góc chung cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.

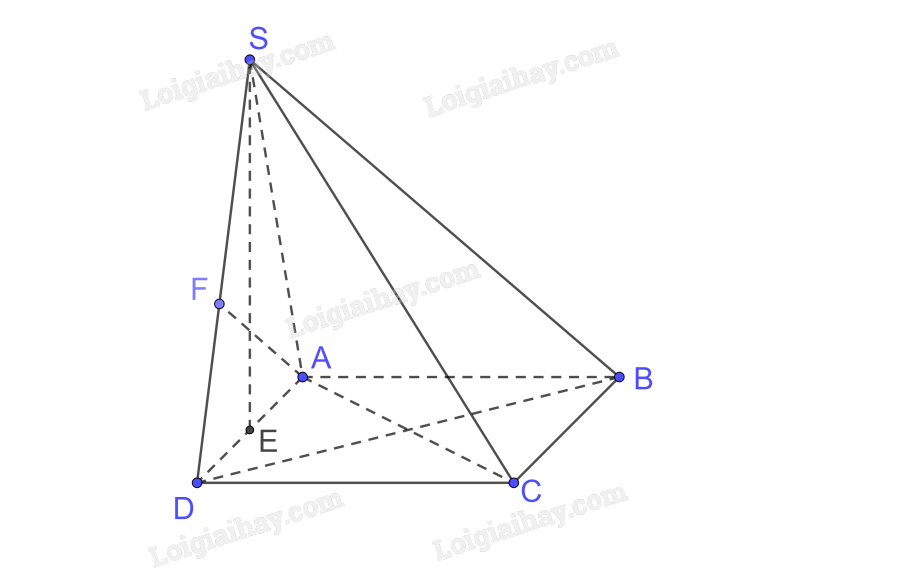
a) Gọi E là trung điểm của AD
\(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\)
Advertisements (Quảng cáo)
Mà tam giác SAD đều
\( \Rightarrow \) \(SE \bot \left( {ABCD} \right)\)
Xét tam giác SDE vuông tại E có
\(SE = \sqrt {S{D^2} - D{E^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
b) Ta có \(AB \bot AD,AB \bot SE\left( {SE \bot \left( {ABCD} \right)} \right) \Rightarrow AB \bot \left( {SAD} \right)\)
Vì BC // AD (ABCD là hình vuông), \(AD \subset \left( {SAD} \right)\) nên BC // (SAD)
\( \Rightarrow \) d(BC, (SAD)) = d(B, (SAD)) = AB = a
c) Trong (SAD) kẻ \(AF \bot SD\)
Có \(AB \bot \left( {SAD} \right),AF \subset \left( {SAD} \right) \Rightarrow AB \bot AF\)
\( \Rightarrow \) d(AB, SD) = AF
Vì tam giác SAD đều nên \(AF = SE = \frac{{a\sqrt 3 }}{2}\)
Vậy \(d\left( {AB,{\rm{ }}SD} \right) = \frac{{a\sqrt 3 }}{2}\)
