Hoạt động 6
Cho hàm số \(y = \tan x\)
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị của hàm số \(y = \tan x\) trên khoảng\(\;\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
|
\(x\) |
\( - \frac{\pi }{3}\) |
\( - \frac{\pi }{4}\) |
\( - \frac{\pi }{6}\) |
0 |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
|
\(y = \tan x\) |
? |
? |
? |
? |
? |
? |
? |
Bằng cách lấy nhiều điểm \(M\left( {x;\tan x} \right)\) với \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = \pi \), ta được đồ thị của hàm số \(y = \tan x\) như hình dưới đây.
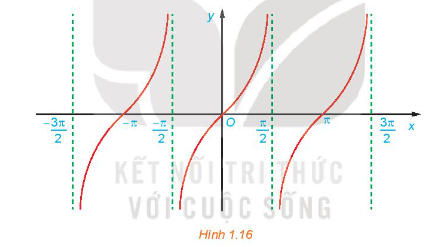
Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số \(y = \tan x\).

Sử dụng định nghĩa hàm số chẵn lẻ
Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.

Advertisements (Quảng cáo)
a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \tan \left( { - x} \right) = - \tan x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \tan x\) là hàm số lẻ.
b)
|
\(x\) |
\( - \frac{\pi }{3}\) |
\( - \frac{\pi }{4}\) |
\( - \frac{\pi }{6}\) |
\(0\) |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
|
\(\tan x\) |
\( - \sqrt 3 \) |
\( - 1\) |
\( - \frac{{\sqrt 3 }}{3}\) |
\(0\) |
\(\frac{{\sqrt 3 }}{3}\) |
\(1\) |
\(\sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).
Luyện tập
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\) để hàm số \(y = \tan x\) nhận giá trị âm.

Nhìn đồ thị để xác định vị trí của y và x

Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)
