Cho tứ diện ABCD, biết AB=BC=AC=BD=a, AD=b, hai mặt phẳng (ACD) và (BCD) vuông góc với nhau.
a) Chứng minh rằng tam giác ACD vuông.
b) Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD.

a)
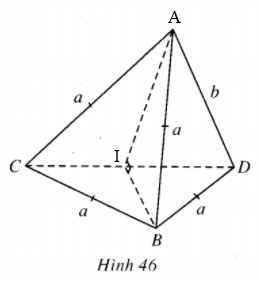
Gọi \(I\) là trung điểm của CD, do BC = BD = a nên \(BI \bot CD.\) Mặt khác \(mp\left( {BCD} \right) \bot mp\left( {ACD} \right)\) nên \(BI \bot mp(ACD).\)
Xét các tam giác vuông AIB và DIB có cạnh góc vuông BI chung, BA = BD, từ đó AI = ID. Vậy ACD là tam giác vuông tại A.
Advertisements (Quảng cáo)
b)
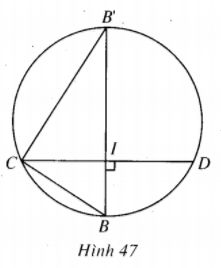
Từ chứng minh trên, ta thấy tâm của mặt cầu ngoại tiếp tứ diện ABCD thuộc BI, do đó, bán kính mặt cầu phải tìm chính là bán kính R của đường tròn ngoại tiếp tam giác BCD.
Dễ thấy CB2=BI.BB’=2R.BI, tức là \(R = {{{a^2}} \over {2BI}}.\)
Mặt khác
\(\eqalign{ & B{I^2} = B{C^2} - {{C{D^2}} \over 4} = {a^2} - {{{a^2} + {b^2}} \over 4} = {{3{a^2} - {b^2}} \over 4} \cr & \Rightarrow BI = {1 \over 2}\sqrt {3{a^2} - {b^2}} ,0 < b < a\sqrt 3 . \cr} \)
Như vậy \(R = {{{a^2}} \over {\sqrt {3{a^2} - {b^2}} }},\)do đó diện tích mặt cầu phải tìm bằng \({{4\pi {a^4}} \over {3{a^2} - {b^2}}}\) với \(0 < b < a\sqrt 3 \).
