Cho hình nón tròn xoay đỉnh S, đáy là đường tròn tâm O. Gọi A là điểm cố định và M là điểm thay đổi cùng thuộc đường tròn đáy hình nón. Đặt
\(AOM{\rm{ }} = {\rm{ }}\alpha \) . Gọi P là góc giữa mp(SAM) và mặt phẳng chứa đáy hình nón ; khoảng cách từ O đến mp(SAM) bằng a.
1. Tính thể tích khối nón đã cho theo a, \(\alpha \),\(\beta \).
2. Xác định điểm M để tam giác SAM có diện tích lớn nhất.
3. Chứng minh rằng hình chiếu H của điểm O trên mp(SAM) thuộc một đường tròn cố định.

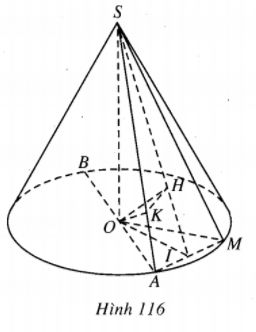
1. Gọi I là trung điểm của AM thì OI \( \bot \)AM và SI \( \bot \)AM từ đó \(\widehat {SIO} = \beta \). Gọi H là hình chiếu của O trên SI thì OH \( \bot \) mp(SAM), từ đó OH = a.
Ta có \(OI = {{OH} \over {\sin \beta }} = {a \over {\sin \beta }}.\)
\(OM = {{OI} \over {\cos {\alpha \over 2}}} = {a \over {sin\beta \cos {\alpha \over 2}}}.\)
Advertisements (Quảng cáo)
\(SO = OI\tan \beta = {a \over {sin\beta }}.tan\beta = {a \over {\cos \beta }}.\)
Từ đó thể tích khối nón đã cho là
\(V = {{\pi {a^3}} \over {3{{\cos }^2}{\alpha \over 2}{{\sin }^2}\beta \cos \beta }}.\)
2. Ta có
Vì SA không đổi nên \({S_{\Delta SAM}}\) lớn nhất \(\Leftrightarrow \sin \widehat {ASM}\) lớn nhất.
Dễ thấy \(\widehat {ASB} > \widehat {ASM}\) (B là điểm đối xứng của A qua O). Vậy có hai trường hợp :
a) \(0 < \widehat {ASB} < {90^0}\) Khi đó , \(\sin \widehat {ASM} \le \sin \widehat {ASB}\) từ đó \(\sin \widehat {ASM}\) lớn nhất khi và chỉ khi M trùng với B.
b) \({90^0} < \widehat {ASB} < {180^0}\) Khi đó \(\sin \widehat {ASM}\) lớn nhất khi và chỉ khi \( \widehat {ASM} = {90^0}\). Vậy có hai vị trí của M trên đường tròn đáy hình nón để diện tích tam giác SAM lớn nhất, đó là hai điểm M sao cho \(\widehat {ASM} = {90^0}\)
3. Vì OH \( \bot \) mp(SAM) nên OH \( \bot \) SA. Vậy H thuộc mp(P) đi qua O và vuông góc với SA tại K. Ta có (P) là mặt phẳng cố định, ngoài ra \(\widehat {OHK} = {90^0}\), tức là H thuộc đường tròn đường kính OK trong mặt phẳng (P) nêu trên, tất nhiên đường tròn này cố định.
