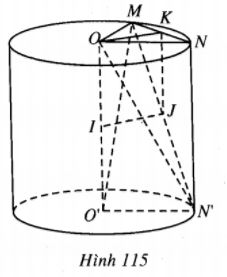
Cho hình trụ có bán kính đáy bằng R, trục là OO‘. Gọi MN là dây cung thay đổi của đường tròn tâm O sao cho MN = R. Kí hiệu N’ là hình chiếu của N trên mặt phẳng chứa đường tròn tâm O’. Gọi I và J lần lượt là trung điểm của OO‘ và MN.
1. Chứng minh rằng IJ là đường vuông góc chung của OO‘ và MN’ và độ dài IJ không đổi.
2. Chứng minh rằng mp(MNN‘) luôn tiếp xúc với một mặt trụ \({\rm T}\) cố định (tức giao của chúng là một đường sinh của \({\rm T}\).

1. Hai tam giác vuông OO‘N‘ và O‘OM có OO‘ chung và O‘N’ = OM nên chúng bằng nhau, từ đó IM = IN‘. Mặt khác JM = JN‘ nên IJ \( \bot \)MN‘.
Advertisements (Quảng cáo)
Cũng dễ thấy các tam giác OMN‘ và O‘N‘M bằng nhau, từ đó OJ = OJ‘; mặt khác IO = IO’ nên IJ \( \bot \) OO’.
Vậy IJ là đường vuông góc chung của OO’ và MN’.
Goi K là trung điểm của MN thì \(OK = {{R\sqrt 3 } \over 2}\) và \(IJ = OK,\) tức là độ dài \(IJ\) không đổi.
2. Từ IJ = \({{R\sqrt 3 } \over 2}\) và IJ \( \bot \) OO’ suy ra điểm J thuộc mặt trụ có trục là OO‘ và bán kính mặt trụ bằng \({{R\sqrt 3 } \over 2}\).
Mặt khác từ IJ \( \bot \) MN‘, IJ \( \bot \) OO‘ suy ra
IJ \( \bot \) mp(MNN‘), tức là mp(MNN‘) tiếp xúc với mặt trụ cố định có trục là OO‘, bán kính \({{R\sqrt 3 } \over 2}\).
