Trong không gian Oxyz cho mp(P) \(:x + 2y{\rm{ }} - {\rm{ }}z + {\rm{ }}5{\rm{ }} = {\rm{ }}0\) và đường thẳng
\(d:{{x + 1} \over 2} = y + 1 = z - 3.\)
1. Tim toạ độ giao điểm A của d và (P).
2. Tính góc \(\alpha \) giữa đường thẳng d và mp(P).
3. Viết phương trình mp(Q) chứa đường thẳng d và vuông góc với mp(P).
4. Viết phương trình hình chiếu vuông góc d’ của d trên mp(P).
5. Viết phương trình đường thẳng nằm trong mp(P) chứa A và vuông góc với đường thẳng d.
6. Viết phương trình mặt cầu có tâm I nằm trên đường thẳng d, tiếp xúc với mp(P) và có bán kính \(R = \sqrt 6 .\)
7. Viết phương trình mp(R) chứa đường thẳng d và tạo với mp(P) một góc nhỏ nhất.

1. Phương trình tham số của d: \(\left\{ {\matrix{ {x = {\rm{ }} - 1{\rm{ }} + {\rm{ }}2t} \hfill \cr {y = {\rm{ }} - 1{\rm{ }} + t} \hfill \cr {z{\rm{ }} = {\rm{ }}3{\rm{ }} + t.} \hfill \cr } } \right.\)
Toạ độ giao điểm A của đường thẳng d với mp(P) thoả mãn hệ :
\(\left\{ {\matrix{ {x = - 1{\rm{ }} + {\rm{ }}2t} \hfill \cr {y{\rm{ }} = - 1{\rm{ }} + t} \hfill \cr {\;z = {\rm{ }}3{\rm{ }} + t} \hfill \cr {x{\rm{ }} + 2y - z + {\rm{ }}5{\rm{ }} = {\rm{ }}0} \hfill \cr } } \right. \)
\(\Rightarrow t = {1 \over 3} \Rightarrow A = \left( { - {1 \over 3}; - {2 \over 3};{{10} \over 3}} \right).\)
2. Gọi \(\alpha \) là góc giữa đường thẳng d và mp(P). d có vectơ chỉ phương \(\overrightarrow {{u_d}} (2;1;1),\) (P) có vectơ pháp tuyến \(\overrightarrow {{n_p}} (1;{\rm{ }}2;{\rm{ }} - {\rm{ }}1)\) nên
\(\sin \alpha = {{\left| {\overrightarrow {{u_d}} .\overrightarrow {{n_P}} } \right|} \over {\left| {\overrightarrow {{u_d}} } \right|.\left| {\overrightarrow {{n_P}} } \right|}} = {{\left| {2 + 2 - 1} \right|} \over {\sqrt {{2^2} + {1^2} + {1^2}} .\sqrt {{1^2} + {2^2} + {{\left( { - 1} \right)}^2}} }}={1 \over 2}\)
\(\Rightarrow \alpha = {30^ \circ }.\)
3. Vì (Q) là mặt phẳng chứa d và vuông góc với mp(P) nên mp(Q) chứa điểm \(\left( { - 1{\rm{ }};{\rm{ }} - 1{\rm{ }};{\rm{ }}3} \right) \in d\) và có vectơ pháp tuyến là
\(\left[ {\overrightarrow {{n_d}} ,\overrightarrow {{n_P}} } \right] = {\rm{ }}\left( { - 3{\rm{ }};{\rm{ }}3{\rm{ }};{\rm{ }}3} \right)\)
Suy ra phương trình mp(Q) là: \(x - y - z + {\rm{ }}3{\rm{ }} = {\rm{ }}0.\)
4. d‘ chính là đường thẳng giao tuyến của hai mặt phẳng (P) và (Q). Vì vậy, điểm \((x{\rm{ }};{\rm{ }}y;{\rm{ }}z) \in d’\) khi và chỉ khi \(\left( {x;y;z} \right)\) thoả mãn hệ
\(\left\{ {\matrix{ {x{\rm{ }} + {\rm{ }}2y{\rm{ }} - {\rm{ }}z{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}0} \hfill \cr {x - y - z + {\rm{ }}3{\rm{ }} = {\rm{ }}0,} \hfill \cr } } \right.\)
hay d‘ có phương trình tham số là :
\(\left\{ \matrix{ x = - {{11} \over 3} + t \hfill \cr y = - {2 \over 3} \hfill \cr z = t. \hfill \cr} \right.\)
5. Gọi \(\Delta \) là đường thẳng nằm trong mpc(P), đi qua điểm \(A\left( { - {1 \over 3}; - {2 \over 3};{{10} \over 3}} \right)\) và vuông góc với đường thẳng d. Khi đó, \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = {1 \over 3}\left[ {\overrightarrow {{u_d}} .\overrightarrow {{n_P}} } \right] = \left( { - 1{\rm{ }};{\rm{ }}1{\rm{ }};{\rm{ }}1} \right)\) nên \(\Delta \) có phương trình chính tắc là
\({{x + {1 \over 3}} \over { - 1}} = y + {2 \over 3} = z - {{10} \over 3}.\)
6. Vì \(I \in d\) nên \(I = {\rm{ }}\left( { - 1 + 2t; - 1{\rm{ }} + {\rm{ }}t;3 + {\rm{ }}t} \right).\)
Mặt cầu tâm I tiếp xúc với mp(P) và có bán kính \(R{\rm{ }} = \sqrt 6 \). Và khi và chỉ khi \(d\left( {I,\left( P \right)} \right){\rm{ }} = {\rm{ }}\sqrt 6 \) hay
\({{\left| { - 1{\rm{ }} + 2t{\rm{ }} - 2{\rm{ }} + 2t{\rm{ }} - 3{\rm{ }} - t{\rm{ }} + 5} \right|} \over {\sqrt {{1^2} + {\rm{ }}{2^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 6 \)
\( < = > \left| {3t - 1} \right|{\rm{ }} = {\rm{ }}6 \Rightarrow \left[ \matrix{ 3t - 1 = 6 \hfill \cr 3t - 1 = - 6 \hfill \cr} \right. \Rightarrow \left[ \matrix{ t = {7 \over 3} \hfill \cr t = - {5 \over 3} \hfill \cr} \right. \)
\(\Rightarrow \left[ \matrix{ I = \left( {{{11} \over 3};{4 \over 3};{{16} \over 3}} \right) \hfill \cr I = \left( { - {{13} \over 3};{{ - 8} \over 3};{4 \over 3}} \right). \hfill \cr} \right.\)
Vậy có hai mặt cầu thoả mản yêu cầu đặt ra là:
Advertisements (Quảng cáo)
\( \left( {{S_1}} \right):{\left( {x - {{11} \over 3}} \right)^2} + {\left( {x - {4 \over 3}} \right)^2} + {\left( {x - {{16} \over 3}} \right)^2} = 6, \)
\(\left( {{S_2}} \right):{\left( {x + {{13} \over 3}} \right)^2} + {\left( {x + {8 \over 3}} \right)^2} + {\left( {x - {4 \over 3}} \right)^2} = 6. \)
7. Cách 1. Ta tìm hai điểm phân biệt thuộc đường thẳng d.
Cho t = 0, ta được \(M( - 1;{\rm{ }} - 1{\rm{ }};{\rm{ }}3) \in d,{\rm{ }}t = {\rm{ }}1,\) ta được \(N\left( {{\rm{ }}1{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ }}4} \right) \in d.\)
Giả sử mặt phẳng (R) cần tìm có phương trình Ax + By + Cz + D = 0 với \({A^2} + {B^2} + {C^2} \ne 0.\)
Vì M, N \( \in \) mp(R)
\(\left\{ \matrix{ - A - B + 3C + D = 0 \hfill \cr A + 4C + D = 0 \hfill \cr} \right. \Rightarrow \left\{ \matrix{ C = - (2A + B) \hfill \cr D = {\rm{ }}7A{\rm{ }} + {\rm{ }}4B. \hfill \cr} \right.\)
Do đó \(\overrightarrow {{n_R}} = {\rm{ }}\left( {A{\rm{ }};{\rm{ }}B; - 2A - {\rm{ }}B} \right).\)
Ta có \(\overrightarrow {{n_P}} = {\rm{ }}\left( {1{\rm{ }};2; - 1} \right).\)
Gọi \(\varphi \) góc giữa hai mặt phẳng (R) và (P) \((0^\circ \le \varphi \le 90^\circ )\) thì:
\(\cos \varphi = {{\left| {A + 2B + 2A + B} \right|} \over {\sqrt 6 \sqrt {{A^2} + {B^2} + {{\left( {2A + B} \right)}^2}} }} = {3 \over {\sqrt 6 }}{{\left| {A + B} \right|} \over {\sqrt {5{A^2} + 2{B^2} + 4AB} }}.\)
Trường hợp A + B = 0, ta có \(\varphi \) = 90° là góc lớn nhất trong các góc có thể có giữa hai mặt phẳng (P) và (R), loại.
Trường hợp \(A + B \ne 0\), ta có
\(\cos \varphi = {3 \over {\sqrt 6 }}\sqrt {{{{{\left( {A + B} \right)}^2}} \over {2{{\left( {A + B} \right)}^2} + 3{A^2}}}} \)
\(= {3 \over {\sqrt 6 }}\sqrt {{1 \over {2 + 3{{\left( {{A \over {A + B}}} \right)}^2}}}} \le {3 \over {\sqrt 6 }}.\sqrt {{1 \over 2}} = {{\sqrt 3 } \over 2},\)
suy ra \(\varphi \ge 30^\circ .\)
Dấu = xảy ra khi A = 0. Khi đó B \( \ne \) 0 (vì nếu B = 0 thì C = 0, vô lí).
Ta chọn B = 1 thì \(C = - (2A + B) = - 1,D{\rm{ }} = {\rm{ }}7A{\rm{ }} + {\rm{ }}4B{\rm{ }} = {\rm{ }}4{\rm{ }}.\)
Vậy mp(R) chứa đường thẳng d và tạo với mp(P) một góc nhỏ nhất (bằng 30°) có phương trình là :
\(y{\rm{ }} - {\rm{ }}z{\rm{ }} + 4{\rm{ }} = {\rm{ }}0.\)
Cách 2. (h. 117)
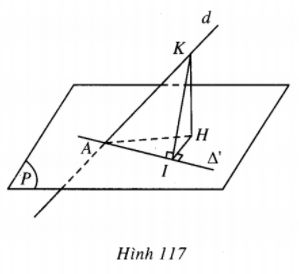
Xét mặt phẳng (Q) thay đổi đi qua đường thẳng d, cắt mp(P) theo giao tuyến \(\Delta ‘.\) Vì \(A{\rm{ }} = {\rm{ }}d{\rm{ }} \cap {\rm{ }}\left( P \right)\) nên \(A{\rm{ }} \in \Delta ‘\).
Lấy một điểm K cố định trên d (K\( \ne \)A). Gọi H là hình chiếu của K trên mp(P), I là hình chiếu của H trên \(\Delta \)’ thì HI và KI cùng vuông góc với \(\Delta \)’
nên là góc giữa mp(P) và mp(Q).
Ta có tan mà KH không đổi khi (Q) thay đổi và \(HI \le HA\) nên
nhỏ nhất <=> tan nhỏ nhất <=> HI lớn nhất <=> I trùng A hay \(\Delta ‘ \bot d\) tại A, tức là \(\Delta \)’ trùng \(\Delta \) (\(\Delta \) nói ở câu 5).
Vậy mp(R) chứa đường thẳng d và tạo với mp(P) một góc nhỏ nhất khi và chỉ khi mp(R) chứa d và \(\Delta \) (\(\Delta \) nằm trên (P), đi qua A và vuông góc với d.
Ta có \(\left[ {\overrightarrow {{u_d}} ,\overrightarrow {{u_\Delta }} } \right] = \left( {0; - {\rm{ }}3;3} \right)\) nên (R) có vectơ pháp tuyến là \(\left( {0{\rm{ }};{\rm{ }}1{\rm{ }};{\rm{ }} - 1} \right).\)
Vì mp(R) đi qua \(A\left( { - {1 \over 3}; - {2 \over 3};{{10} \over 3}} \right)\) nên có phưomg trình là
\(y + {2 \over 3} - \left( {z - {{10} \over 3}} \right) = 0\) hay \(y{\rm{ }} - {\rm{ }}z{\rm{ }} - {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
