Cho hình trụ có trục \({O_1}{O_2}\). Một mặt phẳng \(\left( \alpha \right)\) song song với trục \({O_1}{O_2}\), cắt hình trụ theo thiết diện là hình chữ nhật ABCD. Gọi O là tâm của thiết diện đó. Tính \(\widehat {{O_1}{\rm{O}}{{\rm{O}}_2}}\) biết rằng bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng bán kính đường tròn đáy hình trụ.

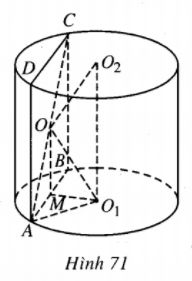
Vì ABCD là hình chữ nhật nên O là trung điểm của AC.
Advertisements (Quảng cáo)
Gọi M là trung điểm của AB thì \({O_1}M \bot AB,OM \bot AB\) và theo giải thiết, AO=AO1.
Hai tam giác vuông MAO và MAO1 có MA chung, \(OA = {O_1}A\) nên \(OM = {O_1}M.\)
Từ đó \(\widehat {{\rm{O}}{{\rm{O}}_1}M}\)= 450, do đó \(\widehat {{\rm{O}}{{\rm{O}}_1}O_2}\) = 450.
Dễ thấy \(\Delta {O_1}O{O_2}\) cân tại O, vậy \(\widehat {{O_1}{\rm{O}}{{\rm{O}}_2}}\) = 900.
