Cho hình trụ có bán kính bằng R, trục OO’ bằng h. Một mặt phẳng (P) thay đổi đi qua O, tạo với đáy hình trụ góc \(\alpha \) cho trước và cắt hai đáy của hình trụ đã cho theo các dây AB và CD ( dây AB đi qua O).
1) Tính diện tích tứ giác ABCD.
2) Chứng minh rằng hình chiếu vuông góc H của điểm O’ trên (P) thuộc một đường tròn cố định.

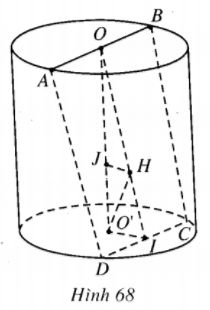
1) Gọi I là trung điểm của CD thì \(O’I \bot CD\), từ đó \(OI \bot CD\). Vậy \(\alpha = \widehat {{\rm{OIO’}}}\).
Dễ thấy \(AB//CD\), tức là ABCD là hình thang. Mặt khác \(OI \bot CD\) nên \(OI \bot AB.\) Vậy ABCD là hình thang cân.
Diện tích S của ABCD được tính bởi
\(S = {1 \over 2}(AB + CD).OI\)
Ta có : \(AB = 2R,OI = {{OO’} \over {\sin \alpha }} = {h \over {\sin \alpha }}.\)
\(\eqalign{ & O’I = OO’\cot \alpha \cr&\Rightarrow ID = \sqrt {O'{D^2} - O'{I^2}} = \sqrt {{R^2} - {h^2}{{\cot }^2}\alpha } \cr & \Rightarrow CD = 2\sqrt {{R^2} - {h^2}{{\cot }^2}\alpha } \cr} \).
Advertisements (Quảng cáo)
Vậy \(S = {1 \over 2}(2R + 2\sqrt {{R^2} - {h^2}{{\cot }^2}\alpha } ).{h \over {\sin \alpha }}\)
\(= (R + \sqrt {{R^2} - {h^2}{{\cot }^2}\alpha } ).{h \over {\sin \alpha }}.\)
2) Trong mặt phẳng (OO’I), kẻ \(O’H \bot OI\) thì H là hình chiếu của O’ trên mp(P).
Xét tam giác vuông O’IH, ta có \(O’H = O’I\sin \alpha = h.\cot \alpha .\sin \alpha = h.c{\rm{os}}\alpha {\rm{.}}\)
Kẻ đường cao HJ của tam giác vuông O’HO thì \(O’J.OO’ = O'{H^2},\)
\( \Rightarrow O’J = {{O'{H^2}} \over {OO’}} = h.{\cos ^2}\alpha ,\) từ đó suy ra J là điểm cố định.
Mặt khác \(H{J^2} = O'{H^2} - O'{J^2} \)
\(= {h^2}.{\cos ^2}\alpha - {h^2}.{\cos ^4}\alpha \)
\(= {h^2}{\cos ^2}\alpha .{\sin ^2}\alpha .\)
Vậy HJ có độ dài không đổi, từ đó ta có điểm H thuộc đường tròn tâm J, bán kính cho trước, trong mặt phẳng vuông góc với OO’ tại J.
Chú ý. Cũng có thể thấy H thuộc mặt trụ T có trục là OO’, bán kính đáy R’ cho trước, cụ thể \(R’ = h.\cos \alpha .\sin \alpha \), đồng thời H thuộc mặt phẳng vuông góc với trục OO’ tại điểm J. Từ đó H thuộc đường tròn là giao của mặt trụ T và mặt phẳng nói trên.
