Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\) nội tiếp trong một hình trụ cho trước, góc giữa đường thẳng \({B_1}D\) và mặt phẳng \(\left( {AB{B_1}{A_1}} \right)\) bằng 300. Khoảng cách từ trục hình trụ đến mặt phẳng \(\left( {AB{B_1}{A_1}} \right)\) bằng \({3 \over 2}a\). Tính thể tích hình hộp đã cho và thể tích hình cầu ngoại tiếp hình hộp, biết đường kính của đáy hình trụ bằng 5a.

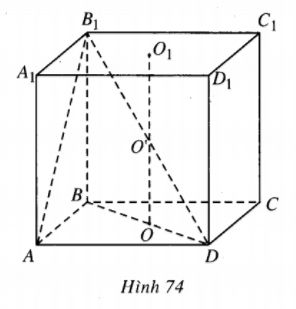
Vì hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\) nội tiếp hình trụ nên \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là hình hộp chữ nhật, trục hình trụ là OO1 ( đoạn nối tâm hai đáy của hình hộp ) và khoảng cách từ OO1 đến mặt phẳng \((AB{B_1}{A_1})\) bằng nửa AD. Từ đó AD = 3a.
BD là đường kính của đường tròn đáy hình trụ nên BD = 5a, suy ra
\(A{B^2} = B{D^2} - A{D^2} = 16{a^2}\), tức là AB = 4a,
Dễ thấy \(\widehat {D{B_1}A}\) là góc giữa \({B_1}D\) và mặt phẳng \((AB{B_1}{A_1})\), theo giả thiết thì \(\widehat {D{B_1}A}\) = 300, từ đó \({B_1}D = 2AD = 6a.\)
Advertisements (Quảng cáo)
Vậy \(BB_1^2 = {B_1}{D^2} - B{D^2} \)
\(\eqalign{
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;= 36{a^2} - 25{a^2} = 11{a^2} \cr
& \Rightarrow B{B_1} = a\sqrt {11} \cr} \)
Do đó thể tích hình hộp đã cho là:
\(V = AB.AD.B{B_1} = 4a.3a.a\sqrt {11} = 12{a^3}\sqrt {11} \)
Gọi O’ là trung điểm của \(O{O_1}\) thì O’ là tâm mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) và bán kính của mặt cầu đólà \(R = {1 \over 2}{B_1}D = 3a.\)
Từ đó thể tích hình cầu phải tìm là
\(V = {4 \over 3}\pi {R^3} = {4 \over 3}\pi .27.{a^3} = 36\pi {a^3}.\)
