Cho tam giác đều ABC cạnh a. Xét đường thẳng \(\Delta \) đi qua A và vuông góc với mp(ABC). Gọi S là điểm bất kì trên \(\Delta \), S khác A.
1) Khi SA=h (h cho trước ), hãy tính diện tích và thể tích của hình cầu ngoại tiếp tứ diện SABC.
2) Gọi A’ là điểm đối xứng với điểm A qua tâm mặt cầu nói trên. Chứng minh rằng khi S thay đổi \(\Delta \) thì A’ thuộc một đường thẳng cố định.

(h.49)
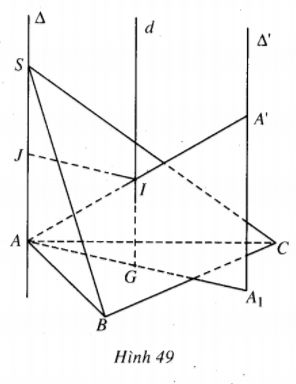
1) Gọi G là trọng tâm của tam giác đều ABC và d là trục của đường tròn ngoại tiếp \(\Delta ABC\) thì \(G \in d\) và \(d//\Delta \). Trong \(mp(\Delta ,d),\) đường trung trực của SA cắt d tại điểm I thì I là tâm của mặt cầu ngoại tiếp tứ diện SABC và R=IA là bán kính của mặt cầu đó.
Advertisements (Quảng cáo)
Dễ thấy \(GI = {1 \over 2}SA = {h \over 2},AG = {{a\sqrt 3 } \over 3},\) từ đó \(I{A^2} = {{{h^2}} \over 4} + {{{a^2}} \over 3} = {1 \over {12}}(4{a^2} + 3{h^2}).\)
Vậy mặt cầu đó có diện tích là
\(S = {\pi \over 3}(4{a^2} + 3{h^2})\)
Và thể tích là
\(V = {4 \over 3}\pi .{\left( {{{\sqrt {4{a^2} + 3{h^2}} } \over {2\sqrt 3 }}} \right)^3} = {\pi \over {18\sqrt 3 }}{(\sqrt {4{a^2} + 3{h^2}} )^3}.\)
2) Khi S thay đổi trên đường thẳng \(\Delta \) thì tâm \(I\) của mặt cầu ấy thay đổi trên đường thẳng d. Mặt khác \(\overrightarrow {AA’} = 2\overrightarrow {AI} ,\) vậy A’ thuộc đường thẳng \(\Delta ‘\) song song với \(\Delta \) và qua điểm \({A_1}\) sao cho \(\overrightarrow {A{A_1}} = 2\overrightarrow {AG} ,\) tức là A’ thuộc đường thẳng cố định \(\Delta ‘.\)
