Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(\widehat B\) = 600. Biết rằng có một hình nón nội tiếp hình chóp đã cho với bán kính đáy là r, góc giữa đường sinh và đáy hình nón là \(\beta .\)
1) Tính diện tích xung quanh và thể tích hình nón.
2) Tính diện tích xung quanh và thể tích hình chóp.

1)
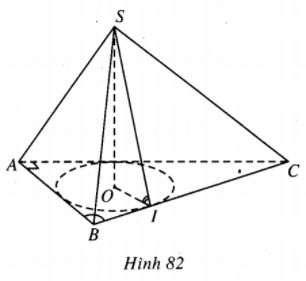
Đáy hình nón trong bài toán là đường tròn nội tiếp tam giác ABC. Đường cao hình nón là SO (S là đỉnh của hình chóp ).
Gọi I là điểm tiếp xúc của BC với đường tròn nội tiếp \(\Delta ABC\) thì \(OI \bot BC\) và \(SI \bot BC\) nên \(\widehat {SIO}\) =\(\beta .\) Khi đó, chiều cao hình nón là
\(h = SO = OI\tan \beta = r\tan \beta ,\)
Độ dài đường sinh hình nón là
\(l = SI = {{OI} \over {\cos \beta }} = {r \over {\cos \beta }}.\)
Vậy diện tích xung quanh của hình nón là
\({S_1} = \pi rl = \pi r.{r \over {\cos \beta }} = {{\pi {r^2}} \over {\cos \beta }}.\)
Advertisements (Quảng cáo)
Thể tích hình nón là
\({V_1} = {1 \over 3}\pi {r^2}h = {1 \over 3}\pi {r^2}.r.\tan \beta = {1 \over 3}\pi {r^3}\tan \beta .\)
2) Dễ thấy ba đường cao của ba mặt bên hình chóp S.ABC bằng nhau và cùng bằng SI.
Diện tích xung quanh của hình chóp là
\({S_2} = {1 \over 2}\left( {AB + AC + BC} \right).SI\)
Mặt khác \(AC = AB\sqrt 3 ,BC = 2AB,\)
\(\eqalign{ & {S_{\Delta ABC}} = {1 \over 2}AB.AC = {1 \over 2}A{B^2}\sqrt 3 , \cr & {S_{\Delta ABC}}= {1 \over 2}\left( {AB + AC + BC} \right).r \cr&\;\;\;\;\;\;\;\;\;\;\;\,= {1 \over 2}\left( {3 + \sqrt 3 } \right).AB.r. \cr} \)
Từ đó \(AB = \left( {\sqrt 3 + 1} \right)r.\)
Vậy diện tích xung quanh của hình chóp S.ABC là
\(\eqalign{ & {S_2} = {1 \over 2}\left( {3 + \sqrt 3 } \right)AB.SI \cr&\;\;\;\;\;= {1 \over 2}\left( {3 + \sqrt 3 } \right)\left( {\sqrt 3 + 1} \right)r.{r \over {\cos \beta }} \cr & \;\;\;\;\;= {{\sqrt 3 } \over 2}{\left( {\sqrt 3 + 1} \right)^2}{{{r^2}} \over {\cos \beta }}. \cr} \)
Thể tích hình chóp S.ABC là
\({V_2} = {1 \over 3}.{1 \over 2}AB.AC.SO = {{\sqrt 3 } \over 6}A{B^2}.SO,\) từ đó
\(\eqalign{ {V_2} &= {{\sqrt 3 } \over 6}{\left( {\sqrt 3 + 1} \right)^2}{r^2}.r\tan \beta \cr & = {{\sqrt 3 } \over 6}{\left( {\sqrt 3 + 1} \right)^2}{r^3}\tan \beta . \cr} \)
