Cho hình lăng trụ đứng có chiều cao h không đổi, đáy là tứ diện ABCD, trong đó A, B, C, D thay đổi và \(\overrightarrow {IA} .\overrightarrow {IC} = \overrightarrow {IB} .\overrightarrow {ID} = - {h^2},\) với I là giao điểm của hai đường chéo. Hãy xác định giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp hình lăng trụ đó.

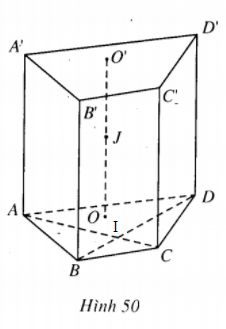
(h.50)
Vì \(\overrightarrow {IA} .\overrightarrow {IC} = \overrightarrow {IB} .\overrightarrow {ID} \) nên ABCD là tứ giác nội tiếp đường tròn .
Mặt khác, hình lăng trụ đã cho là lăng trụ đứng nên hình lăng trụ đó có mặt cầu ngoại tiếp.
Advertisements (Quảng cáo)
Kí hiệu O, O’ lần lượt là tâm đường tròn ngoại tiếp đáy ABCD và A’B’C’D’ của hình lăng trụ và gọi J là trung diểm của OO’ thì J là tâm mặt cầu phải tìm và bán kính của mặt cầu là JA.
Mặt khác \(J{A^2} = J{O^2} + A{O^2} = {{{h^2}} \over 4} + A{O^2}.\)
Từ đó, bán kính mặt cầu đạt giá trị nhỏ nhất khi và chỉ khi bán kính đường tròn ngoại tiếp đáy ABCD đạt giá trị nhỏ nhất.
Ta có \({h^2} = - \overrightarrow {IA} .\overrightarrow {IC} = - \overrightarrow {IB} .\overrightarrow {ID} = A{O^2} - I{O^2}.\)
\( \Rightarrow A{O^2} = {h^2} + I{O^2}\)
Từ đó, \(A{O^2}\) đạt giá trị nhỏ nhất khi và chỉ khi IO nhỏ nhất, điều này xảy ra khi và chỉ khi \(O \equiv I,\) lúc đó \(A{O^2} = {h^2}\) và giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp hình lăng trụ bằng \(J{A^2} = {{h\sqrt 5 } \over 2}.\)
