Cho tam giác đều ABC cạnh a. Gọi (P) là mặt phẳng qua cạnh BC và vuông góc với mp(ABC). Gọi (C) là đường tròn đường kính BC trong mp(P) và S là điểm bất kì thuộc (C). Khi S thay đổi trên (C), chứng minh rằng :
1) \(S{A^2} + S{B^2} + S{C^2}\) không đổi ;
2) Tâm mặt cầu ngoại tiếp tứ diện SABC là điểm cố định ( nếu S khác B, C).

(h.51)
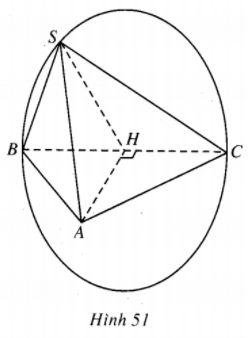
1) Vì \(\widehat {BSC} = \) \({90^ \circ }\) nên \(S{B^2} + S{C^2} = B{C^2} = {a^2}.\)
Gọi H là trung điểm của BC thì
Advertisements (Quảng cáo)
\(SH = {1 \over 2}BC = {a \over 2}\) và \(AH \bot BC.\)
Mặt khác, \(\left( P \right) \bot mp\left( {ABC} \right)\) và cắt mặt phẳng này theo giao tuyến BC nên \(AH \bot (P).\)
Từ đó \(S{A^2} = S{H^2} + A{H^2} = {{{a^2}} \over 4} + {{3{a^2}} \over 4} = {a^2}.\)
Vậy \(S{A^2} + S{B^2} + S{C^2} = {a^2} + {a^2} = 2{a^2}.\)
2) Vì HB = HC = HS, \(AH \bot mp(SBC)\) nên đường thẳng AH là trục của đường tròn ngoại tiếp \(\Delta SBC\).
Do đó, tâm mặt cầu ngoại tiếp tứ diện SABC thuộc AH. Mặt khác, ABC là tam giác đều nên tâm mặt cầu đó chính là tâm đường tròn ngoại tiếp tam giác ABC và bán kính mặt cầu bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Điều ấy khẳng định rằng mặt cầu ngoại tiếp tứ diện SABC là cố định.
