Cho tứ diện đều ABCD, AA1 là một dường cao của tứ diện. Gọi I là trung điểm của AA1. Mặt phẳng (BCI) chia tứ diện đã cho thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó.

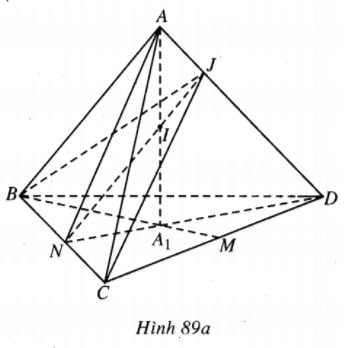
Gọi N là trung điểm của BC và J là giao điểm của NI với AD, khi đó mp(BCI) chia tứ diện đã cho thành hai tứ diện BCDJ và ABCJ.
Dễ thấy \({\rm{AJ = }}{1 \over 4}AD.\)
Vì \({\rm{A}}{{\rm{A}}_1} \bot mp(BCD)\) nên mọi điểm thuộc \({\rm{A}}{{\rm{A}}_1}\) cách đều B,C, D. Khi đó, tâm O1 của mặt cầu ngoại tiếp tứ diện BCDJ là giao điểm của \({\rm{A}}{{\rm{A}}_1}\) với đường trung trực của JD( xét trong mp(\({\rm{A}}{{\rm{A}}_1}D\))).
Tương tự như trên, tâm O2 của mặt cầu ngoại tiếp tứ diện ABCJ là giao của với đường trung trực của AJ ( xét trong mp(ADD1))(DD1 là đường cao kẻ từ đỉnh D của tứ diện ABCD).
Gọi E và F lần lượt là trung điểm của DJ và AJ. Xét tứ giác nội tiếp \({O_1}{A_1}DE\) (hình 89b), ta có
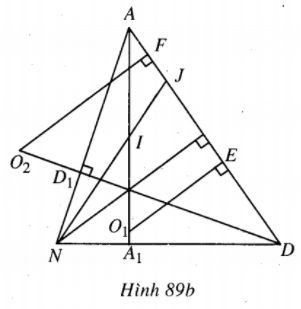
\(\eqalign{ & AE.AD = A{O_1}{\rm{.A}}{{\rm{A}}_1} \cr & \Rightarrow A{O_1} = {{AE.AD} \over {A{A_1}}}. \cr} \)
Mặt khác
\({\rm{A}}{{\rm{A}}_1} = {{a\sqrt 6 } \over 3},AE = {a \over 4} + {{3a} \over 8} = {{5a} \over 8}.\)
Từ đó
\(A{O_1} = {{5a.a} \over {8.{{a\sqrt 6 } \over 3}}} = {{5a\sqrt 6 } \over {16}}.\)
Advertisements (Quảng cáo)
Và do đó \({A_1}{O_1} = {A_1}A - A{O_1} \)
\(= {{a\sqrt 6 } \over 3} - {{5a\sqrt 6 } \over {16}} = {{a\sqrt 6 } \over {48}}\)
Vậy bán kính \({R_1}\) của mặt cầu ngoại tiếp tứ diện BCDJ là
\(\eqalign{ & R_1^2 = {O_1}{D^2} = {A_1}O_1^2 + {A_1}{D^2}\cr&\;\;\;\;\;\; = {{6{a^2}} \over {{{48}^2}}} + {{3{a^2}} \over 9} = {{{a^2}} \over {48.8}} + {{{a^2}} \over 3} = {{129.{a^2}} \over {48.8}} \cr & \Rightarrow {R_1} = {{a\sqrt {129} } \over {8\sqrt 6 }}. \cr} \)
Từ giác \({O_2}{D_1}FA\) nội tiếp đường tròn nên
\({\rm{D}}{{\rm{D}}_1}.D{O_2} = DF.DA \Rightarrow D{O_2} = {{DF.DA} \over {D{D_1}}}.\)
Mặt khác
\(DF = {{3a} \over 4} + {a \over 8} = {{7a} \over 8},DA = a,{\rm{D}}{{\rm{D}}_1} = {{a\sqrt 6 } \over 3},\) từ đó
\(D{O_2} = {{{{7a} \over 8}.a} \over {{{a\sqrt 6 } \over 3}}} = {{21a\sqrt 6 } \over {8.6}} = {{7a\sqrt 6 } \over {16}}.\)
Suy ra \({{\rm{D}}_1}{{\rm{O}}_2} = {{7a\sqrt 6 } \over {16}} - {{a\sqrt 6 } \over 3} = {{5a\sqrt 6 } \over {48}}\) và do đó, bán kính \({R_2}\) của mặt cầu ngoại tiếp tứ diện ABCJ là
\(R_2^2 = {O_2}A_2^2 = {O_2}D_1^2 + {D_1}{A^2} \)
\(= {{25{a^2}.6} \over {{{48}^2}}} + {\left( {{{a\sqrt 3 } \over 3}} \right)^2} \)
\(= {{25{a^2}} \over {48.8}} + {{{a^2}} \over 3} = {{153{a^2}} \over {48.8}},\)
Từ đó \({R_2} = {{a\sqrt {153} } \over {8\sqrt 6 }}.\) Vậy \({{{R_1}} \over {{R_2}}} = {{a\sqrt {129} } \over {8\sqrt 6 }}:{{a\sqrt {153} } \over {8\sqrt 6 }} = \sqrt {{{43} \over {51}}} .\)
