Trong không gian cho các điểm A, B, C lần lượt thuộc các tia Ox, Oỵ, Oz vuông góc với nhau từng đôi một sao cho \(OA = a\;(a > {\rm{ }}0),OB = a\sqrt 2 ,\) \(OC{\rm{ }} = {\rm{ }}c{\rm{ }}\;(c{\rm{ }} > 0).\) Gọi D là đỉnh đối diện với O của hình chữ nhật AOBD và M là trung điểm của đoạn BC. (P) là mặt phẳng đi qua AM và cắt mặt phẳng (OCD) theo một đường thẳng vuông góc với đường thẳng AM.
a) Gọi E là giao điểm của (P) với đường thẳng OC, tính độ dài đoạn thẳng OE.
b) Tính tỉ số thể tích của hai khối đa diện được tạo thành khi cắt khối chóp C.AOBD bởi mặt phẳng (P).
c) Tính khoảng cách từ điểm C đến mặt phẳng (P).

(h.111)
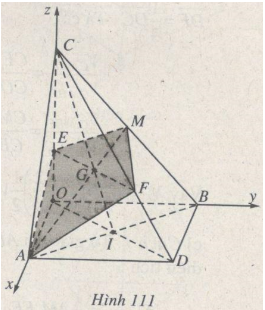
a) Cách 1: Giả sử I là giao điểm của OD và AB, F là giao điểm củá mp(P) với CD. Khi đó dễ thấy ba đường thẳng EF, AM và CI đồng quy tại trọng tâm G của tam giác ABC.
Đặt \(\overrightarrow {OE} {\rm{ }} = {\rm{ }}k.\overrightarrow {OC} .\)
Từ giả thiết GA \( \bot \) GE, ta có \(\overrightarrow {GA} .\overrightarrow {GE} = 0.\)
Mặt khác \(\overrightarrow {GA} .\overrightarrow {GE} = \left( {\overrightarrow {OA} - \overrightarrow {OG} } \right).\left( {\overrightarrow {OE} - \overrightarrow {OG} } \right)\)
\( = \left[ {\overrightarrow {OA} - {1 \over 3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)} \right].\)
\(\left[ {k\overrightarrow {OC} - {1 \over 3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)} \right]\)
\( = - {1 \over 3}\overrightarrow {O{A^2}} + {1 \over 9}\overrightarrow {O{A^2}} + {1 \over 9}\overrightarrow {O{B^2}} + {1 \over 9}\overrightarrow {O{C^2}} - {1 \over 3}k\overrightarrow {O{C^2}} \) (Vì \(\overrightarrow {OA} .\overrightarrow {OB} = \overrightarrow {OB} .\overrightarrow {OC} = \overrightarrow {OC} .\overrightarrow {OA} = 0\))
\( =- {1 \over 3}{a^2} + {1 \over 9}{a^2} + {2 \over 9}{a^2} + {1 \over 9}{c^2} - {k \over 3}{c^2}\) (vì \(OA = a,OB = a\sqrt 2 ,OC = c\)).
Vậy \(\overrightarrow {GA} .\overrightarrow {GE} = 0 \Leftrightarrow {1 \over 9}{c^2} - {k \over 3}{c^2} = 0 \Leftrightarrow k = {1 \over 3}.\) Vậy \(OE = {1 \over 3}c.\)
Advertisements (Quảng cáo)
Cách 2. Chọn hệ toạ độ Đề-các vuông góc Oxyz như hình 111 thì
\(A{\rm{ }} = {\rm{ }}\left( {a{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ 0}}} \right),{\rm{ }}B{\rm{ }} = \left( {0;a\sqrt 2 ;0} \right){\rm{, }}D = {\rm{ }}\left( {a{\rm{ }};a\sqrt 2 ;{\rm{ }}0} \right),\)
\({\rm{ }}C = {\rm{ }}\left( {0{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ }}c} \right),\)\(M = \left( {0;{{a\sqrt 2 } \over 2};{c \over 2}} \right),\) Sử dụng giả thiết của bài toán, ta lập được phương trình của mặt phẳng (P) là \(c\sqrt 2 \left( {x{\rm{ }} - a} \right) - {\rm{ }}cy{\rm{ }} + {\rm{ }}3a\sqrt 2 z{\rm{ }} = {\rm{ }}0\).
Giao điếm của (P) với trục Oz là \(E{\rm{ }} = {\rm{ }}\left( {0{\rm{ }};{\rm{ }}0{\rm{ }};{c \over 3}} \right)\), suy ra \(OE{\rm{ }} = {c \over 3}.\)
b) Vì \(\overrightarrow {OE} = {1 \over 3}\overrightarrow {OC} \) , giao tuyến EF của (P) với (OCD) song song với OD nên \(\overrightarrow {DF} = {1 \over 3}\overrightarrow {DC} \) . Ta có
\(\eqalign{ & {{{V_{C.AEF}}} \over {{V_{C.AOD}}}} = {{CE} \over {CO}}.{{CF} \over {CD}} = {2 \over 3}.{2 \over 3} = {4 \over 9}, \cr & {{{V_{C.MEF}}} \over {{V_{C.BOD}}}} = {{CM} \over {CB}}.{{CE} \over {CO}}.{{CF} \over {CD}} = {1 \over 2}.{2 \over 3}.{2 \over 3} = {2 \over 9}. \cr} \)
Vậy \({V_{C.AEMF}} = \left( {{4 \over 9} + {2 \over 9}} \right){1 \over 2}{V_{C.AOBD}} = {1 \over 3}{V_{C.AOBD}}\), từ đó \({{{V_{C.AEMF}}} \over {{V_{AEMFDBO}}}} = {1 \over 2}.\)
c) Cách 1. Tứ giác lồi AEMF có các đường chéo AM, EF vuông góc nên có diện tích :
\({S_{AEMF}} = {1 \over 2}AM.FE\)
\( = {1 \over 2}\sqrt {A{O^2} + O{J^2} + J{M^2}} .{2 \over 3}OD\) (J là trung điểm của OB)
\( = {1 \over 2}\sqrt {{a^2} + {{{a^2}} \over 2} + {{{c^2}} \over 4}} .{2 \over 3}\sqrt {{a^2} + 2{a^2}} = {{\sqrt 3 } \over 6}a\sqrt {6{a^2} + {c^2}} .\)
Vậy khoảng cách từ C đến mp(P) là
\(d\left( {C{\rm{ }},{\rm{ }}\left( P \right)} \right) = {{3{V_{C.AEMF}}} \over {{S_{AEMF}}}} = {{{a^2}c{{\sqrt 2 } \over 3}} \over {{{\sqrt 3 } \over 6}a\sqrt {6{a^2} + {c^2}} }} = {{2ac\sqrt 6 } \over {3\sqrt {6{a^2} + {c^2}} }}.\)
Cách 2. Sử dụng cách 2 của câu a), ta tính được khoảng cách từ điểm \(C(0{\rm{ }};{\rm{ }}0{\rm{ }};c)\) đến mp(P) có phương trình \(c\sqrt 2 \left( {x - a} \right) - cy{\rm{ }} + {\rm{ }}3a\sqrt 2 z{\rm{ }} = {\rm{ }}0\) là
\(d\left( {C,\left( P \right)} \right) = {{\left| { - ac\sqrt 2 + 3ac\sqrt 2 } \right|} \over {\sqrt {2{c^2} + {c^2} + {\rm{ }}18{a^2}} }} = {{2ac\sqrt 6 } \over {3\sqrt {{c^2} + {\rm{ 6}}{a^2}} }}.\)
