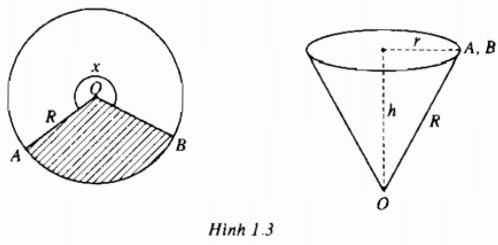
Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình 1.3) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của một hình quạt còn lại với nhau để được một cái phễu có dạng một hình nón. Gọi x là góc ở tâm của hình quạt tròn dùng làm phễu (h.1.3), \(0 < x < 2\pi \)
a) Hãy biểu diễn hán kính r của hình tròn đáy và đường cao h của hình nón theo R và x.
b) Tính thể tích hình nón theo R và x.
c) Tìm x để hình nón có thể tích lớn nhất và tính giá trị lớn nhất đó.
Giải
a) Vì độ dài của đường tròn đáy hình nón bằng độ dài \(\overparen{AB}\) của quạt tròn dùng làm phễu, nên ta có
\(2\pi r = Rx\)
Do đó
\(r = {{Rx} \over {2\pi }}\)
và \(h = \sqrt {{R^2} - {r^2}} = \sqrt {{R^2} - {{{R^2}{x^2}} \over {4{\pi ^2}}}} = {R \over {2\pi }}\sqrt {4{\pi ^2} - {x^2}} \)
Advertisements (Quảng cáo)
b) Thể tích hình nón là
\(V = {1 \over 3}\pi {r^2}h = {{{R^3}} \over {24{\pi ^2}}}{x^2}\sqrt {4{\pi ^2} - {x^2}} ,0 < x < 2\pi \)
c) Ta tìm \(x \in \left( {0;2\pi } \right)\) sao cho tại đó V đạt giá trị lớn nhất
\(V’ = {{{R^3}} \over {24{\pi ^2}}}.{{x\left( {8{\pi ^2} - 3{x^2}} \right)} \over {\sqrt {4{\pi ^2} - {x^2}} }}\)
Với \(0 < x < 2\pi \), ta có
\(V’ = 0 \Leftrightarrow 8{\pi ^2} - 3{x^2} = 0 \Leftrightarrow x = {{2\sqrt 6 } \over 3}\pi \approx 1,63\pi \)
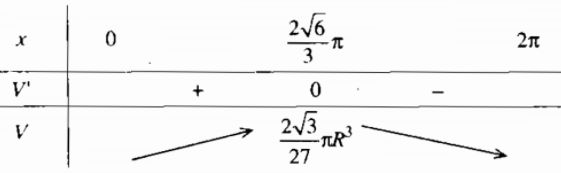
Hình nón có thể tích lớn nhất khi \(x = {{2\sqrt 6\pi } \over 3} \approx 1,63\pi \)
\(\mathop {\max }\limits_{x \in \left( {0;2\pi } \right)} V = V({{2\sqrt 6 \pi} \over 3}) = {{2\sqrt 3 } \over {27}}\pi {R^3}\)
Sacbaitap.com
